Introduction
In previous courses, you have studied different types of similar figures. In a previous resource, you examined similarity relationships using scale factor and proportion.
In this resource, you will investigate dilations, which are enlargements and reductions of given figures.

An enlargement is a type of dilation that results in a larger figure. Enlargements are used in photography to print a larger picture from a particular image. Enlargements are also used in architecture where a pattern in a small part of a building is taken in a larger part of the building.

A reduction is a type of dilation that results in a smaller figure. A camera works by creating an image of a real-life scene that is proportionally smaller. This image is called a reduction. Video game designers may also use reductions in order to create sharper and better graphics.
Determining the Scale Factor for Dilations
The key to describing dilations is knowing the scale factor that relates the preimage, or the original object, to the image, or the enlarged or reduced object. In this part of the lesson, you will investigate how to determine the scale factor that is being used for a given dilation.
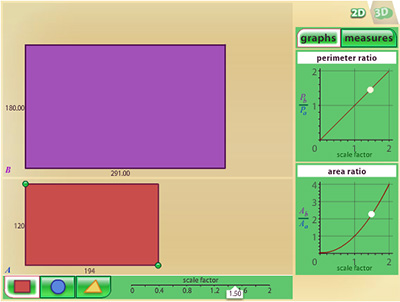
Click on the screenshot below and use the interactive tool to dilate quadrilateral A. The slider that is labeled "Scale Factor" controls the scale factor used to generate the purple quadrilateral, B, from the red quadrilateral, A. Record your observations in your notes.
Additional Instructions: Click on the 2D tab found on the upper right hand corner of the interactive.
Click on the red rectangle in the lower left-hand corner. Use the scale factor slider to change the size of the purple shape in relation to the red one.
The dimensions of the red shape can be changed by clicking and dragging a green vertex. Graphs and measures can be observed on the right panel by clicking on the tabs.
- What do you notice about the ratio of the lengths of two corresponding sides and the scale factor of the dilation?
- If you know the lengths of two corresponding sides in two similar figures, how can you determine the scale factor?
The table below indicates whether each scale factor generates an enlargement or a reduction.
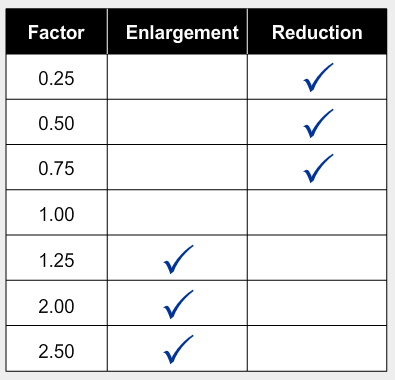
How can you determine whether a scale factor will generate an enlargement or a reduction?
Practice
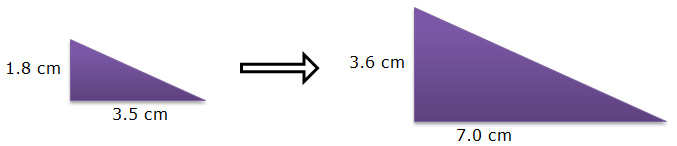
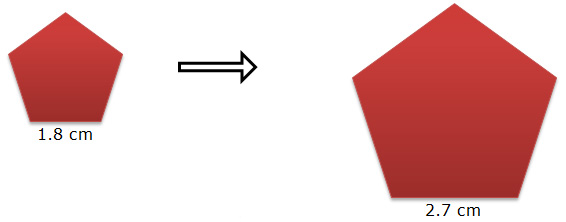
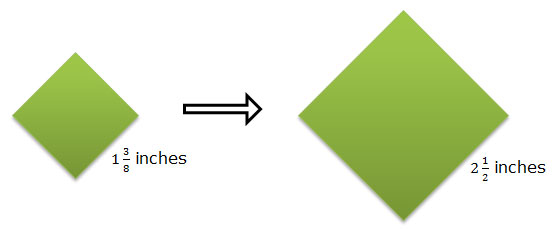
Using Scale Factor to Determine Measurements in Dilations
If you know an original dimension and a scale factor of dilation, you can use that information to determine measurements in the dilated figure.
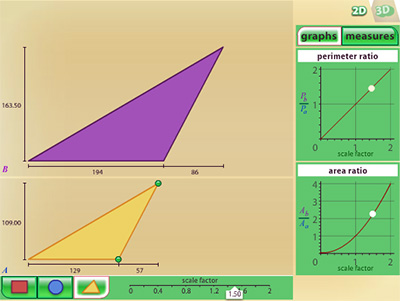
Click on the screenshot below and use the interactive tool to dilate rectangle A. Use the properties of a rectangle to calculate the perimeter of A. Then use the dilated dimensions, as well as the properties of a rectangle, to calculate the perimeter of B. Click on the "measures" tab to check your answers.
What is the ratio of the dilated perimeter to the original perimeter?
Now use the same interactive, but change the shape to a triangle. Move the vertex to make a right triangle, and dilate triangle A. Use the properties of a right triangle to calculate the perimeter of A. Then use the dilated dimensions, as well as the properties of a right triangle, to calculate the perimeter of triangle B. Click on the "measures" tab to check your answers.
What is the ratio of the dilated perimeter to the original perimeter?
Practice
Parallelogram ABCD is dilated by a scale factor of 0.75 in order to generate parallelogram PQRS.
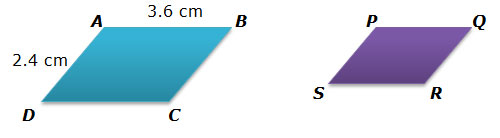
- Determine the lengths of sides PQ and SP in parallelogram PQRS.
- Determine the perimeter of parallelogram PQRS.
Summary
Dilations can be either an enlargement, which results in a figure that is larger than the original figure, or a reduction, which results in a figure that is smaller than the original figure.
Because dilations generate similar figures, you can use properties of similarity (specifically, proportional relationships) to determine measurements.
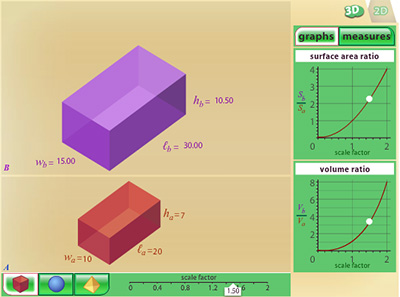
For an additional challenge, click on the image below and choose the 3D tab to explore dilations in three dimensions.