Introduction
In previous grades, you used different models and procedures to generate equivalent fractions.
Equivalent fractions are related in that they represent the same part of the same whole, but the numerators and denominators are different. Equivalent fractions are related by a scale factor that can be multiplied by the numerator and denominator.
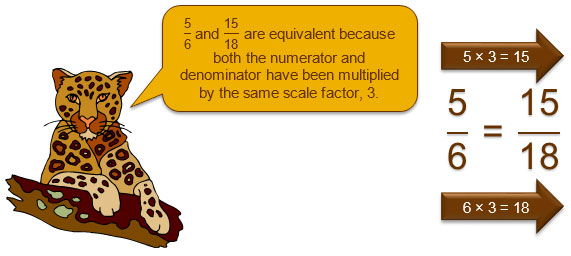
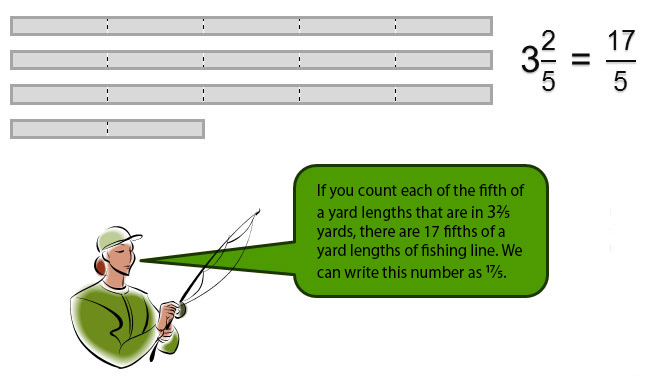
You can also have an improper fraction and a mixed number that are equivalent. For example, if Mary has yards of fishing line, she also has yards of fishing line.
In this lesson, you will investigate other ways to write equivalent forms of rational numbers, including fractions, decimals, and percents.
Relationships Between Fractions and Decimals
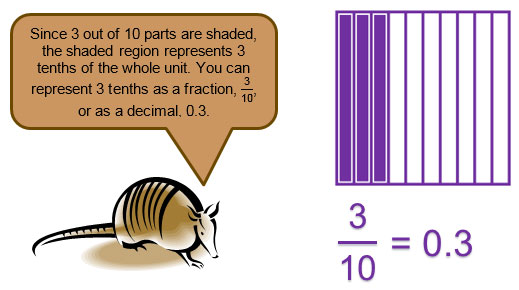
In this part of the lesson, you will focus on the relationships between fractions and decimals and how to generate one form of a rational number from the other. Fractions and decimals are two ways that you can represent a quantity that is a part of a whole. For example, the model below shows a square that represents one whole. The square is broken into ten equal parts, three of which are shaded.

Lone Star General Store uses both fractions and decimals to represent information about pricing. Shortly after opening their website, the managers decided to have a sale on online e-book downloads.
Prices of the e-books are given with decimal numbers. Some of the prices are shown below.

Before you can calculate the discounted price of an e-book, you need to convert the fractional discount to a decimal number, or convert the decimal number price to a fraction.

Click through the interactive below to see how Damian used equivalent fractions to rewrite as a fraction with a denominator of 10.
Pause and Reflect
Damian wants to write the fraction as a decimal number. He knows to generate an equivalent fraction with a denominator of 100. What scale factor does Damian need to use? What will be the resulting equivalent fraction and decimal number?
Check Your Answer
Damian wants to write the fraction as a decimal number. He knows to generate an equivalent fraction with a denominator of 1000. What scale factor does Damian need to use? What will be the resulting equivalent fraction and decimal number?
Check Your Answer
Not all fractions can be rewritten as equivalent fractions with a denominator of 10, 100, or 1000. For those fractions, you need an alternate method.

Pause and Reflect
In general, what are two ways that you can generate a decimal number from a fraction?
Check Your Answer
If you know a decimal, how can you use place value to write an equivalent fraction? For example, how could you write 0.78 as a fraction?
Check Your Answer
Relationships Between Decimals and Percents
In the previous section, you used models to show how the same part of a whole can be represented with both a fraction and a decimal. In this part of the lesson, you will focus on how you can represent the same part of a whole with equivalent decimal numbers or percents. Recall that a percent is a rational number that describes the number of parts per 100. For example, the Texas state sales tax rate is 6.25%. This means that for every dollar—or 100 cents—of a sale, 6.25 cents are added to the purchase total in order to pay a state sales tax.

Use the sliders in the interactive to show the relationship between a number written as a percent and the number written as a decimal. Click on the horizontal slider to change the tens digit in the percent and the vertical slide to change the ones digit in the percent.
Use the interactive to create a model for the given percents. Copy and paste the table below into a word processing or spreadsheet program or app. Record the equivalent decimal number in the table. Use your table to answer the questions that follow.
|
Percent
|
Decimal Number
|
|
25%
|
|
|
63%
|
|
|
78%
|
|
|
18%
|
- What patterns do you notice in the completed table?
- What relationship is there between the tens digit of the percent and the tenths digit of the decimal number?
- What relationship is there between the ones digit of the percent and the hundredths digit of the decimal number?
- What number could you multiply or divide the percent by (without the percent sign) to obtain the decimal number?
- What number could you multiply or divide the decimal number by to obtain the percent?
Pause and Reflect
- A percent is a part of the whole given in terms of the number of parts per 100. How does the definition of a percent appear in the relationship between a percent and its equivalent decimal number?
- If the percent is greater than 100%, such as 245%, how will you convert the percent to a decimal number?
Practice
- In a recent year, the cost of gasoline showed a 29.6% increase in price. What is this number represented as a decimal?
- A grocery store is advertising produce at a 20% discount and milk for 0.9 times the original price. Which item is being sold for a greater portion of its original price?
- In a local toy store, a radio-controlled car costs 1.25 as much as a car that is not radio-controlled. What is the relationship between the cost of the radio-controlled car and car that is not radio-controlled, 1.25, written as a percent?
Relationships Between Fractions and Percents
In the previous sections, you used models to generate equivalent fractions from decimals (and vice versa) and to generate equivalent percents from decimals (and vice versa). In this part of the lesson, you will focus on equivalent forms of fractions and percents.
Lone Star General Store uses both percents and fractions to advertise discounts on their merchandise. Look at one part of this week’s sales flyer.

Because Lone Star General Store uses both percents and fractions, you need to know how to write a percent as a fraction so that you can compare the discounts. You also need to know how to write a fraction as a percent.
Use the slider in the interactive below to show the relationship between a number written as a percent and the number written as a fraction.
Use the interactive to complete the table below. Copy and paste the table below into a word processing or spreadsheet program or app. Record the equivalent fraction from the interactive in the table. Then, generate an equivalent fraction with a denominator of 100. Use your table to answer the questions that follow.
|
Percent
|
Simplified Fraction
|
Fraction with Denominator = 100
|
|
10%
|
||
|
20%
|
||
|
40%
|
||
|
45%
|
||
|
60%
|
||
|
75%
|
||
|
84%
|
||
|
90%
|
- What patterns do you notice in the completed table?
- What relationship is there between the numerator of the fraction with a denominator of 100 and the percent?
- To generate a fraction from a percent, what number could you use as the denominator of a fraction?
- How can you simplify a fraction to one that is written in lowest terms?
- If you have a fraction with a denominator that is not 100, how could you generate an equivalent percent for that fraction?
Pause and Reflect
- A percent is a part of the whole given in terms of the number of parts per 100. How does the definition of a percent appear in the relationship between a percent and its equivalent fraction?
Check Your Answer - If the percent were greater than 100%, such as 245%, how would you convert the percent to a fraction?
Check Your Answer
Practice
The Lone Star General Store has a new sale coming up for next week. According to their sales flyer, the following discounts will be offered.

Summary
In this lesson, you used models to show how different forms of rational numbers (fractions, decimals, and percents) can be used to represent the same part of a whole.

The model below shows the number of people who like the new giraffe exhibit.

Since there are 64 squares out of 100 shaded, this ratio can be written as a fraction, decimal, or percent.
You also investigated several different ways to generate equivalent forms of a rational number if you are given a fraction, decimal, or percent.
To review the procedures used for generating equivalent forms of rational numbers, click on the representation that you wish to generate from the representation that you know. For example, if you have a fraction and wish to generate an equivalent decimal number, click on the “Fraction → Decimal” button to see a procedure you may use.