Volume is a very important geometric attribute of 3-dimensional figures.

The volume of a 3-dimensional figure is the number of cubic units that will completely fill the space inside the figure.

You have also seen the formulas for determining the volume of prisms, pyramids, cylinders, cones, and spheres.

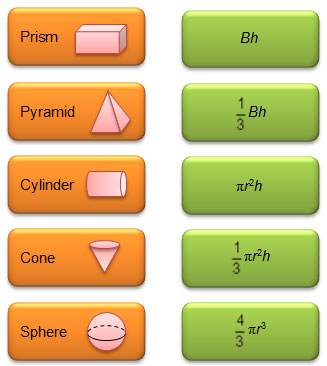
In this resource, you will practice solving application problems involving volume of 3-dimensional figures. You may find these formulas to be useful, so keep them or a collection of mathematics reference materials handy!

The Sweet Surprises Candy Factory specializes in custom-molded chocolate candies. The factory supervisor purchases chocolate in bars that are shaped like rectangular prisms, which are then sliced and melted according to which types of candies need to be made.

The dimensions of the original chocolate bars are shown.

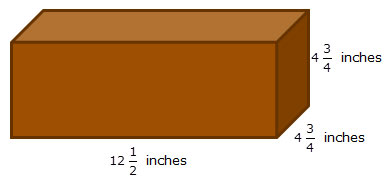
First, we need to determine the volume of chocolate, in cubic inches, contained in one chocolate bar.

In the activity below, drag the dimensions to the appropriate place in the formula to calculate the volume of the chocolate bar.

Now that you have correctly identified the dimensions, calculate the volume of the chocolate bar.

For one recipe, the chef needs $180\frac{1}{2}$ cubic inches of chocolate. To obtain this amount of chocolate, the chef will slice a chocolate bar as shown in the diagram.

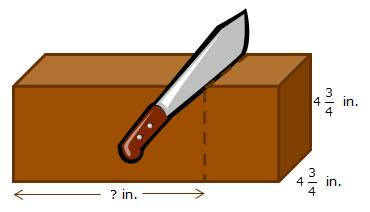
What will be the resulting length of the chocolate bar that the chef will melt to use for his recipe?

Volumes of Pyramids

A customer has ordered chocolate candies that are solid and in the shape of square pyramids. The dimensions in the schematic are shown in the figure below.

In the activity below, drag the dimensions to the appropriate place in the formula to calculate the volume of the candies.

Now that you have correctly identified the dimensions, calculate the volume of one of the pyramid-shaped chocolate candies.

Bonus Question:
How many of the pyramid-shaped candies could be made from one full-sized chocolate bar?

Practice

1. A vase is in the shape of a rectangular prism and has the dimensions shown below.

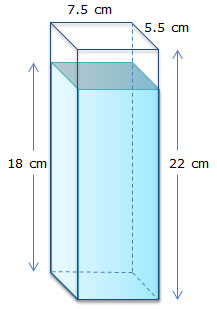
If the vase is filled with water to a height of 18 cm, what is the volume of water inside the vase? 

2. A tent is shaped like an isosceles triangular prism.

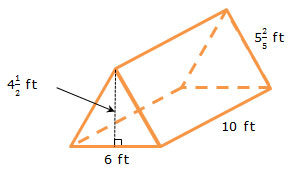
Calculate the volume of air that will be contained inside the tent.

3. A metronome is made from wood and is shaped like a square pyramid with the dimensions shown.

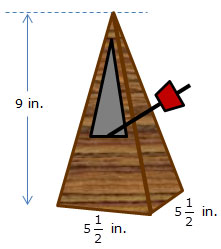
Calculate the volume of wood required to construct the metronome.

A terrarium is a miniature landscape built within a container. Much like an aquarium is a tank that contains water, rocks, and fish, a terrarium contains soil, plants, and sometimes even small animals.

Lashonda owns a company that builds and sells terrariums. The terrariums that she sells come in the shapes of cylinders, cones, and spheres.

A cylindrical terrarium contains a desert landscape, including sand and cacti. The dimensions of the terrarium are shown. The cylinder has a diameter of 24 inches and a height of 18 inches and contains sand in the bottom to a depth of 4 inches.

Now that you have correctly identified the dimensions, calculate the volume of sand required for one desert terrarium.

Conical Terrariums

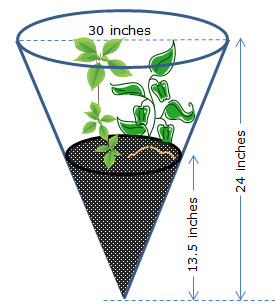
A cone-shaped, or conical, terrarium contains a woodland landscape, including soil and plants you might find in a forest. The dimensions of the terrarium are shown. The cone has a diameter of 30 inches and a height of 24 inches and contains soil in the bottom to a depth of 13.5 inches.

Lashonda needs to know how much space this cone-shaped woodland terrarium will occupy. Drag the dimensions to the appropriate place in the formula to calculate the volume of the woodland terrarium.

Now that you have correctly identified the dimensions, calculate the volume of the woodland terrarium.

Spherical Terrariums

A spherical terrarium contains a tropical landscape, including soil and tropical plants such as ferns and flowers. The dimensions of the terrarium are shown. The sphere has a diameter of 28 inches and contains soil in the bottom to a depth of 14 inches.

Lashonda needs to know the total volume of this spherical tropical terrarium. Drag the dimensions to the appropriate place in the formula to calculate the volume of the tropical terrarium.

Now that you have correctly identified the dimensions, calculate the volume of the tropical terrarium.

Practice

1. A vase is in the shape of a cylinder and has the dimensions shown.

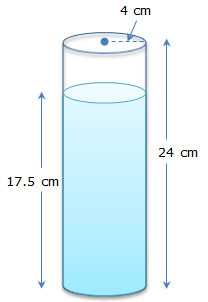
If the vase is filled with water to a height of 17.5 cm, what is the volume of water inside the vase?

2. A cone-shaped drinking cup has the dimensions shown.

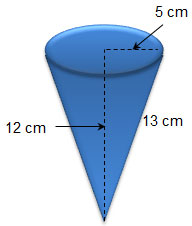
When the cup is completely filled, how much water will it hold?

3. A bowling ball has a diameter of 8 inches and is made of a combination of plastic and resin. How much material is required to manufacture one bowling ball, excluding the space for the finger holes?

In this lesson, you have applied volume formulas in order to solve problems involving the volume of prisms, pyramids, cylinders, cones, and spheres.

Use the summary chart to drag and drop the formulas to the appropriate 3-dimensional figure.