Introduction
As you have seen in previous grades or lessons, the area of a figure is the amount of flat space that the figure covers. Area is measured in square units, such as square inches or square centimeters.
Area formulas with which you may be familiar include the following.
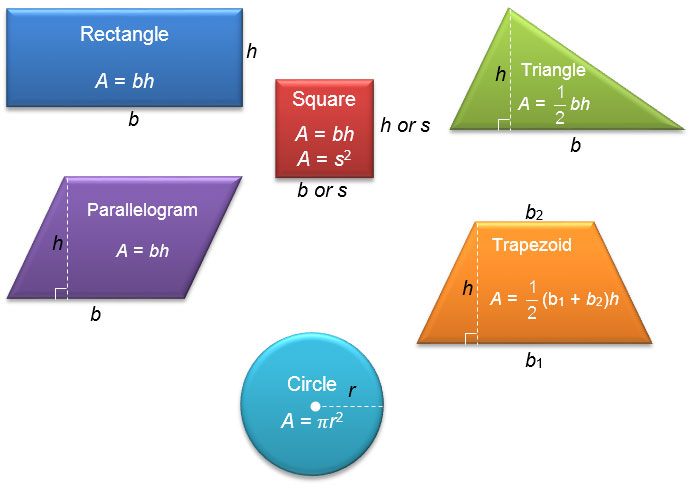
Not all figures that you will encounter can be neatly described as one of these polygons or as a circle. Instead, they may be part of a figure, such as a semicircle, or they may be made up of several polygons. If a figure is made up of several polygons, parts of polygons, or parts of circles, then that figure is called a composite figure. In this lesson, you will learn how to determine the area of composite figures.
Breaking Down Composite Figures
In the introduction, you reviewed area formulas that you can use to calculate the area of particular polygons and circles. In the real world, not every figure can be cleanly classified as a rectangle, parallelogram, triangle, or trapezoid. Consider the following real-world objects for which it is useful to be able to determine the area.

Source: Landscape Design Advisor, Flickr

Source: Liben(121), Dezidor, Wikimedia Commons
In order to calculate the area of these figures and many more, you need to be able to solve problems that involve composite figures.
The border of a playground is shown below. Look at the second slide to see how one student partitioned the figure.

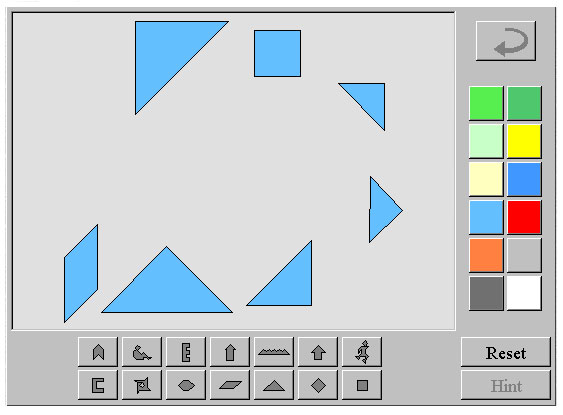
One way that you can break down a figure into triangles, squares, and parallelograms is to use tangrams. Tangrams are tiles from a Chinese puzzle that can be rearranged to create geometric designs.
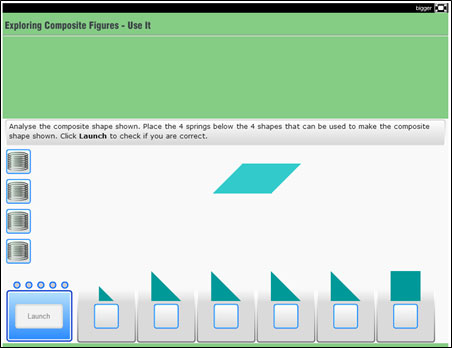
 Use the tangrams pieces in the interactive below to recreate the composite figures beneath the link to the tangrams interactive. Click on the image to open the interactive, which will open in a new browser tab or window. Then, click and drag on the tangram pieces until you have recreated the composite figure. There may be more than one possible answer. (Note: Use Firefox or Internet Explorer as your browser for this interactive.)
Use the tangrams pieces in the interactive below to recreate the composite figures beneath the link to the tangrams interactive. Click on the image to open the interactive, which will open in a new browser tab or window. Then, click and drag on the tangram pieces until you have recreated the composite figure. There may be more than one possible answer. (Note: Use Firefox or Internet Explorer as your browser for this interactive.)
Pause and Reflect
- When you are partitioning a composite figure into triangles, what patterns should you look for?
- If you were partitioning a figure into rectangles, what would you need to look for?
Practice
For questions 1–3, partition the composite figure into a combination of rectangles, triangles, parallelograms, trapezoids, or circles (including semicircles or quarter circles). There may be more than one possible answer. You may assume that angles appearing to be right angles are right angles.
Matching Area Formulas with Figures
In the last section, you practiced different ways to partition a composite figure into rectangles, triangles, parallelograms, trapezoids, squares, circles, semicircles, or quarter circles. In this section, you will take those smaller parts and identify area formulas necessary to calculate the area of each component region of the composite figure.
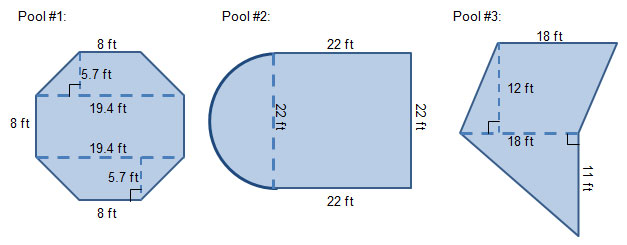
A swimming pool company offers several designs of swimming pools, including the ones shown below.

Nedra is in charge of calculating the area of the surface of each pool. The animation below shows how Nedra divided the composite figure representing each swimming pool into regions. These regions should have simple area formulas. See how she did it below.
The actual dimensions for each pool are shown below. Calculate the area of each pool by calculating the area of each component region, and then determine the sum of the areas.
Check Your Answer Pool #1
Check Your Answer Pool #2
Check Your Answer Pool #3
Pause and Reflect
- Thinking about area formulas, which type of polygon or circle is it easier to break a composite figure into in order to calculate the area?
- Why is it sometimes possible to break a composite figure into different polygons?
Practice
For questions 1–3, each composite figure is broken into different component regions. Identify the area formula required to calculate the area of each component region.
Solving Problems Involving Composite Figures
In the last two sections, you practiced breaking a composite figure into component regions. These regions should have simple area formulas. In this section, you will apply that knowledge to solving both mathematical and real-world problems.

Sometimes, a composite figure contains a hole or a region that must be removed when determining the area of the composite figure.
What operation describes removing, or taking away, a quantity?
Use the interactive below to practice solving problems involving composite figures that are made up of polygons or parts of circles. On screen directions will be provided. You will be asked to identify the component polygons and/or circles. Identify the necessary area formulas, and calculate the area of each component polygon and/or circle. Work through several problems before returning to the lesson. When you click the image below, the interactive will appear in a new browser tab or window.
Sometimes, you have to remove a region from a composite figure when you are determining its area.
Watch the video below to see how to use subtraction when determining the area of a composite figure.
Pause and Reflect
How can you tell whether you need to add or subtract areas of component regions of composite figures?
Summary
In this lesson, you learned how to apply what you know about the area of triangles, certain quadrilaterals, and circles to solving problems involving composite figures. A composite figure is a shape whose classification is not readily apparent, but whose area can be determined by breaking it into component regions with simple area formulas.
The area of composite figures can be determined using either addition or subtraction.