Introduction
In previous grades you learned how to add, subtract, multiply, and divide. You’ve learned how important math is and how it is used in everyday life.
Below are some everyday math experiences. Click on a rectangle below to review an expression representing the everyday experience. The operation associated with the term and an example will appear.
In this lesson, you will see other examples of how these skills are used in our everyday lives, including balancing a bank register. You will also simplify expressions using the order of operations and learn more about why the order of operations is used.
Addition and Subtraction

Even though addition and subtraction are skills learned at a young age, they are used throughout your life. Let’s look at bank registers, which are used by bank customers to keep track of the amount of money in their bank account.
- A bank register is a table the bank usually provides when an account is opened. It is used to record all transactions and to keep track of the current account balance.
- A transaction can be a deposit or a withdrawal.
- A deposit is when a bank customer places more money into his or her account, such as depositing a paycheck.
- A withdrawal is when a bank customer takes money out of his or her account. Withdrawals can be in the form of a check, a cash withdrawal from the bank, or an online bill payment.
Below is an example of how to use a bank register.

Samantha wants to save for a new computer. She has \($\)10.00 saved, so she is babysitting to earn more money. Each time Samantha babysits, she adds her earnings to her previous savings.
This week Samantha babysat three times. On the first day, she received \($\)25.00. On the second day, she received \($\)36.00, and on the third day, she received \($\)15.50.

She has to pay her parents \($\)1.75 each time they transport her to or from her babysitting jobs, so Samantha subtracts her transportation expenses from her earnings to obtain a current balance of the money she has saved.
Samantha decided she would enter the information into a bank register. This way she can have an accurate current balance of her savings.
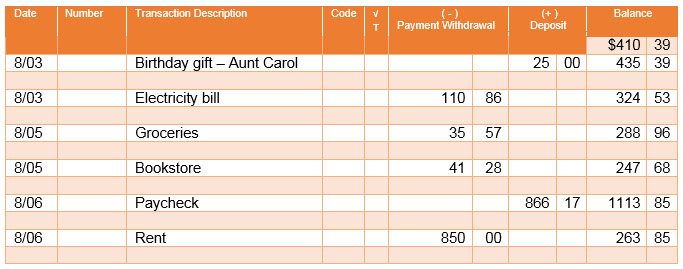
Below is the check register Samantha uses to keep track of her current balance. Click on the arrow to see how Samantha filled in the check register.
- How are mathematical operations represented in the check register?
- Samantha pays her parents at the end of the month, but she uses the check register to keep a daily total. How can she determine the total amount she would pay her parents at the end of the month?
Multiplication and Division

In this section, you will review numerical expressions that include exponents and prime factorization.
Source: Clipboard/Lined Paper, algotruneman, Open Clipart
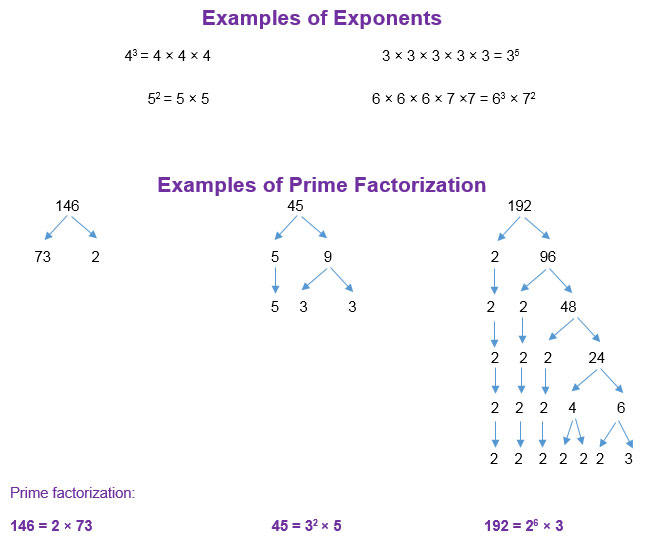
Use the interactive to review and practice exponents and prime factorization. Match cards that have equivalent expressions.
Using the information from the interactive, answer the following questions:
- Which pairs of numbers are prime numbers and which pairs are composite numbers?
- Explain why the prime factorizations used exponents.
Practice
A. Find the prime factorization for each number.
B. Write it in exponential notation if possible.
- 300
- 195
- 693
- 357
Order of Operations
In the past two sections, you reviewed addition, subtraction, multiplication, and division. In this section, you will notice that when simplifying expressions, there is a specific mathematical order.
To begin this part of the lesson, use a calculator or app to simplify the following expression. Once you have done so, continue the lesson to see how other students simplified the expression.

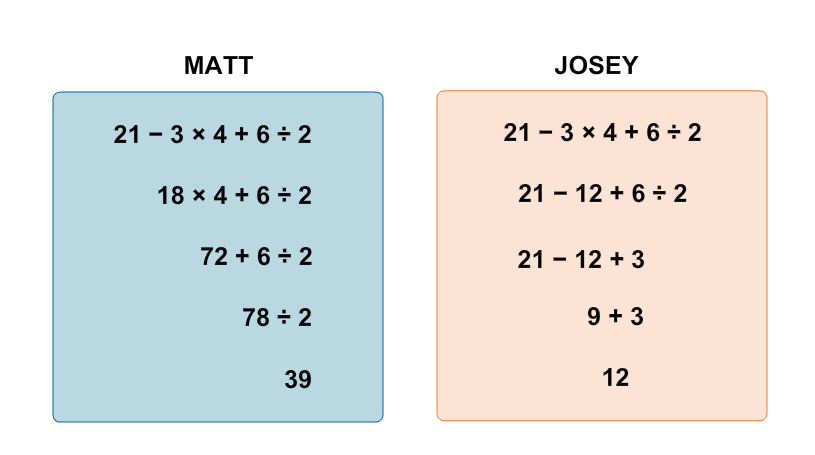
Matt and Josey simplified the same expression below and got different results. Compare your solution to theirs.
Knowing How to Determine the Correct Answer
As you can see, it is possible to get different answers if we don’t have directions to follow. The directions used for simplifying expressions are called the order of operations.
In the above example, four operations were performed in the expression: subtraction, multiplication, addition, and division. How do you know which one to do first? Matt started on the left and worked straight through to the right. Josey started multiplying first. See the correct order of operations below.
The order of operations was developed to provide consistent directions for solving math problems. Basically, start with grouping, and then do the most powerful to the least powerful operation.
Look at Matt and Josey’s work again, and then answer the following questions.

- Describe how they both started and if their first steps would make a difference in their answer.
- Explain why it is important to use order of operations when solving problems.
- Is it possible to simplify an expression and obtain the same result by not following the order of operations?
Practice
Simplify each expression below using the order of operations.
- 131 + 26 ÷ 2 − 16 × 6
- 21 × 3 − 24 ÷ 8 − 8 × 5
- 25 × 3 ÷ 5 + 15 × 4 ÷ 3 − 5 × 7
Order of Operations with Grouping
In the previous section, you used the order of operations to simplify basic expressions. Now, you will look at more ways to remember the order of operations and practice simplifying a few more expressions.


Another way to remember the order of operations is GEMA. Click on each letter of the acronym to see what each letter represents.
Finish simplifying the expression.
Practice
Simplify each expression below using the order of operations.
- 7 + ((9 + 3) × 6)
- (52 + (8 ÷ 2 + 22)) − 22
- (8 + 55 − 3) ÷ 5 + 42
Summary
In this lesson, you reviewed addition and subtraction with decimal numbers by balancing a check register. You learned how to use exponents and prime factorization to represent whole numbers. You also applied the order of operations in order to simplify numerical expressions.