Test Prep
Multiple Choice
9.1 Work, Power, and the Work–Energy Theorem
The work–energy theorem states that the change in the kinetic energy of an object is equal to what?
- The work done on the object
- The force applied to the object
- The loss of the object’s potential energy
- The object’s total mechanical energy minus its kinetic energy
A runner at the start of a race generates 250 W of power as he accelerates to 5 m/s . If the runner has a mass of 60 kg, how long did it take him to reach that speed?
- 0.33 s
- 0.83 s
- 1.2 s
- 3.0 s
A car’s engine generates 100,000 W of power as it exerts a force of 10,000 N. How long does it take the car to travel 100 m?
- 0.001 s
- 0.01 s
- 10 s
- 1,000 s
9.2 Mechanical Energy and Conservation of Energy
- The constant is missing.
- The term should not be squared.
- The expression should be divided by .
- The energy lost to friction has not been subtracted.
- Initial PE is transformed to KE until the javelin reaches the high point of its arc. On the way back down, KE is transformed into PE. At every point in the flight, mechanical energy is being transformed into heat energy.
- Initial KE is transformed to PE until the javelin reaches the high point of its arc. On the way back down, PE is transformed into KE. At every point in the flight, mechanical energy is being transformed into heat energy.
- Initial PE is transformed to KE until the javelin reaches the high point of its arc. On the way back down, there is no transformation of mechanical energy. At every point in the flight, mechanical energy is being transformed into heat energy.
- Initial KE is transformed to PE until the javelin reaches the high point of its arc. On the way back down, there is no transformation of mechanical energy. At every point in the flight, mechanical energy is being transformed into heat energy.
- At the bottom of the slope kinetic energy is at its maximum value and potential energy is at its minimum value.
- At the bottom of the slope potential energy is at its maximum value and kinetic energy is at its minimum value.
- At the bottom of the slope both kinetic and potential energy reach their maximum values
- At the bottom of the slope both kinetic and potential energy reach their minimum values.
9.3 Simple Machines
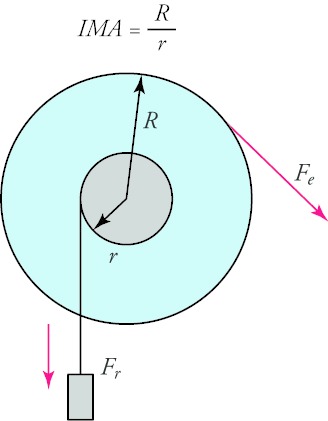
A large radius divided by a small radius is the expression used to calculate the IMA of what?
- A screw
- A pulley
- A wheel and axle
- An inclined plane.
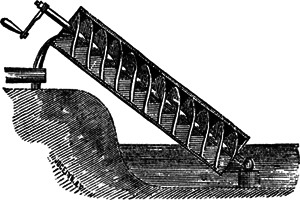
- The crank is a wedge in which the IMA is the length of the tube divided by the radius of the tube. The applied force is the effort force and the weight of the water is the resistance force.
- The crank is an inclined plane in which the IMA is the length of the tube divided by the radius of the tube. The applied force is the effort force and the weight of the water is the resistance force.
- The crank is a wheel and axle. The effort force of the crank becomes the resistance force of the screw.
- The crank is a wheel and axle. The resistance force of the crank becomes the effort force of the screw.
How hard would you have to pull on the rope to lift a 120 N load?
How many meters of rope would you have to pull out of the system to lift the load 1 m?
- 480 N
4 m
- 480 N
m
- 30 N
4 m
- 30 N
m
Short Answer
9.1 Work, Power, and the Work–Energy Theorem
- Raising an object to a higher elevation does work as it increases its PE; increasing the speed of an object does work as it increases its KE.
- Raising an object to a higher elevation does work as it increases its KE; increasing the speed of an object does work as it increases its PE.
- Raising an object to a higher elevation does work as it increases its PE; decreasing the speed of an object does work as it increases its KE.
- Raising an object to a higher elevation does work as it increases its KE; decreasing the speed of an object does work as it increases its PE.
True or false—While riding a bicycle up a gentle hill, it is fairly easy to increase your potential energy, but to increase your kinetic energy would make you feel exhausted.
- True
- False
Which statement best explains why running on a track with constant speed at 3 m/s is not work, but climbing a mountain at 1 m/s is work?
- At constant speed, change in the kinetic energy is zero but climbing a mountain produces change in the potential energy.
- At constant speed, change in the potential energy is zero, but climbing a mountain produces change in the kinetic energy.
- At constant speed, change in the kinetic energy is finite, but climbing a mountain produces no change in the potential energy.
- At constant speed, change in the potential energy is finite, but climbing a mountain produces no change in the kinetic energy.
- is your speed at the top of the hill, and is your speed at the bottom.
- is your speed at the bottom of the hill, and is your speed at the top.
- is your displacement at the top of the hill, and is your displacement at the bottom.
- is your displacement at the bottom of the hill, and is your displacement at the top.
9.2 Mechanical Energy and Conservation of Energy
True or false—The formula for gravitational potential energy can be used to explain why joules, J , are equivalent to kg × mg2 / s2 . Show your work.
- True
- False
- Because kinetic energy is directly proportional to the square of the velocity.
- Because kinetic energy is inversely proportional to the square of the velocity.
- Because kinetic energy is directly proportional to the fourth power of the velocity.
- Because kinetic energy is inversely proportional to the fourth power of the velocity.
- When the coin hits the ground, the ground gains potential energy that quickly changes to thermal energy.
- When the coin hits the ground, the ground gains kinetic energy that quickly changes to thermal energy.
- When the coin hits the ground, the ground gains thermal energy that quickly changes to kinetic energy.
- When the coin hits the ground, the ground gains thermal energy that quickly changes to potential energy.
True or false—A marble rolls down a slope from height h1 and up another slope to height h2, where (h2h1). The difference mg(h1 – h2) is equal to the heat lost due to the friction.
- True
- False
9.3 Simple Machines


- The resistance arm is shorter in case of the inclined plane.
- The effort arm is shorter in case of the inclined plane.
- The area of contact is greater in case of the inclined plane.
- The area of contact is less in case of the inclined plane.
- The wheel on the wheelbarrow has no fulcrum.
- The center of the axle is not the fulcrum for the wheels of a wheelbarrow.
- The wheelbarrow differs in the way in which load is attached to the axle.
- The wheelbarrow has less resistance force than a wheel and axle design.
A worker pulls down on one end of the rope of a pulley system with a force of 75 N to raise a hay bale tied to the other end of the rope. If she pulls the rope down 2.0 m and the bale raises 1.0 m, what else would you have to know to calculate the efficiency of the pulley system?
- the weight of the worker
- the weight of the hay bale
- the radius of the pulley
- the height of the pulley from ground
True or false—A boy pushed a box with a weight of 300 N up a ramp. He said that, because the ramp was 1.0 m high and 3.0 m long, he must have been pushing with force of exactly 100 N.
- True
- False
Extended Response
9.1 Work, Power, and the Work–Energy Theorem
Work can be negative as well as positive because an object or system can do work on its surroundings as well as have work done on it. Which of the following statements describes:
- A gasoline engine burns less fuel at a slower speed.
Solar cells capture sunlight to generate electricity.
- A hybrid car charges its batteries as it decelerates.
Falling water turns a turbine to generate electricity.
- Airplane flaps use air resistance to slow down for landing.
Rising steam turns a turbine to generate electricity.
- An electric train requires less electrical energy as it decelerates.
A parachute captures air to slow a skydiver’s fall.
A boy is pulling a girl in a child’s wagon at a constant speed. He begins to pull harder, which increases the speed of the wagon. Which of the following describes two ways you could calculate the change in energy of the wagon and girl if you had all the information you needed?
- Calculate work done from the force and the velocity.
Calculate work done from the change in the potential energy of the system.
- Calculate work done from the force and the displacement.
Calculate work done from the change in the potential energy of the system.
- Calculate work done from the force and the velocity.
Calculate work done from the change in the kinetic energy of the system.
- Calculate work done from the force and the displacement.
Calculate work done from the change in the kinetic energy of the system.
9.2 Mechanical Energy and Conservation of Energy
Acceleration due to gravity on the moon is 1.6 m/s2 or about 16% of the value of g on Earth.
- The velocity of the rock as it hits the ground would be 5.0 m/s. Due to the lack of air friction, there would be complete transformation of the potential energy into the kinetic energy as the rock hits the moon’s surface.
- The velocity of the rock as it hits the ground would be 5.0 m/s. Due to the lack of air friction, there would be incomplete transformation of the potential energy into the kinetic energy as the rock hits the moon’s surface.
- The velocity of the rock as it hits the ground would be 12 m/s. Due to the lack of air friction, there would be complete transformation of the potential energy into the kinetic energy as the rock hits the moon’s surface.
- The velocity of the rock as it hits the ground would be 12 m/s. Due to the lack of air friction, there would be incomplete transformation of the potential energy into the kinetic energy as the rock hits the moon’s surface.
- As the boulder rolls down the mountainside, KE is converted to PE. As the boulder rolls up the opposite slope, PE is converted to KE. The boulder rolls only partway up the ridge because some of the PE has been converted to thermal energy due to friction.
- As the boulder rolls down the mountainside, KE is converted to PE. As the boulder rolls up the opposite slope, KE is converted to PE. The boulder rolls only partway up the ridge because some of the PE has been converted to thermal energy due to friction.
- As the boulder rolls down the mountainside, PE is converted to KE. As the boulder rolls up the opposite slope, PE is converted to KE. The boulder rolls only partway up the ridge because some of the PE has been converted to thermal energy due to friction.
- As the boulder rolls down the mountainside, PE is converted to KE. As the boulder rolls up the opposite slope, KE is converted to PE. The boulder rolls only partway up the ridge because some of the PE has been converted to thermal energy due to friction.
9.3 Simple Machines
- Each handle and its attached blade is a lever with the fulcrum at the hinge. Each blade is a wedge.
The IMA of a lever would be the length of the handle divided by the length of the blade. The IMA of the wedges would be the length of the blade divided by its width.
- Each handle and its attached to blade is a lever with the fulcrum at the end. Each blade is a wedge.
The IMA of a lever would be the length of the handle divided by the length of the blade. The IMA of the wedges would be the length of the blade divided by its width.
- Each handle and its attached blade is a lever with the fulcrum at the hinge. Each blade is a wedge.
The IMA of a lever would be the length of the handle multiplied by the length of the blade. The IMA of the wedges would be the length of the blade multiplied by its width.
- Each handle and its attached blade is a lever with the fulcrum at the end. Each blade is a wedge.
The IMA of a lever would be the length of the handle multiplied by the length of the blade. The IMA of the wedges would be the length of the blade multiplied by its width.
A wooden crate is pulled up a ramp that is 1.0 m high and 6.0 m long. The crate is attached to a rope that is wound around an axle with a radius of 0.020 m . The axle is turned by a 0.20 m long handle. What is the overall IMA of the complex machine?
- 6
- 10
- 16
- 60

