Introduction
In English, "poly-" is a prefix that means "many." Polynomials are groups of monomials that have been added or subtracted. Monomials are things like 3x, 4y, and the number 5. All of the monomials are called "terms of a polynomial."
Some polynomials have two terms and are called binomials. An example of a binomial is 5x - 2.
Some polynomials have three terms and are called trinomials. An example of trinomial is 9x2 + 6x + 1.
Simplifying Polynomials
Polynomials can be simplified in several ways:
- Algebra tiles can be used to represent polynomials so that they can be simplified.
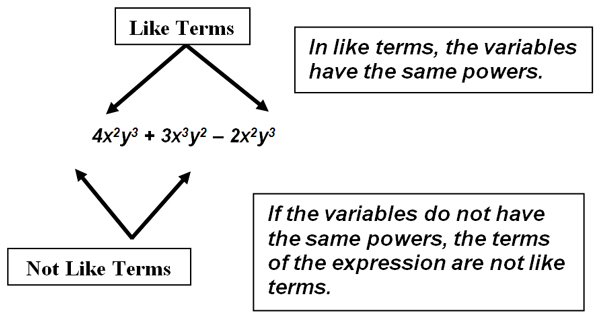
- Combining like terms can be used to simplify polynomials. Like terms are monomials which have exactly the same variables with exactly the same exponents. For example, 2x and 3x are like terms. 2x2 and 3x are not like terms because the exponents are different.
- Polynomials can be simplified by using the distributive property to distribute the term on the outside of the parentheses by multiplying it by everything inside the parentheses.
- You can simplify polynomials by using FOIL to multiply binomials times binomials.
We're going to focus on simplifying polynomials using algebra tiles, combining like terms, and using the distributive property.
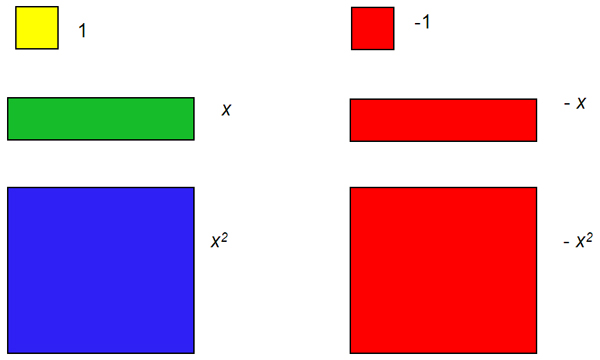
Algebra Tiles
One way to simplify polynomials is by using algebra tiles. Different algebra tiles represent different values. These are the different algebra tiles and their values.
Simplifying Like Terms
You can simplify a polynomial by adding or subtracting like terms. Let's look at the trinomial below and identify the like terms.
Distributive Property
Sometimes before we add or subtract to simplify the polynomial, we have to multiply. When this happens, we use the distributive property.
Let's look at an example of simplifying with and without the distributive property.
Example 1
Consider solving the equation :
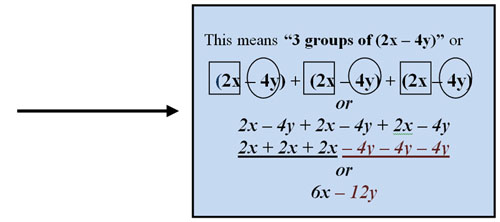
You can also solve this equation with the distributive property:
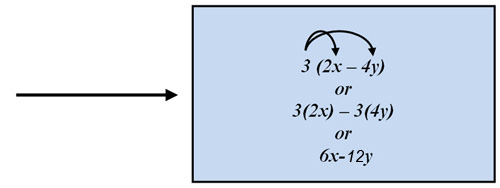
Which way was simpler to use?
Polynomial Perimeters
Now that you can simplify polynomials, let's apply your knowledge to solving perimeter problems.
Can you work through this problem? Kevin is going to frame a rectangular picture with the dimensions shown. How much wood does he need to make a frame?
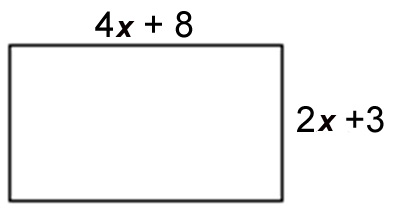
How do you find a perimeter of a rectangle? Do you remember the formula?
The formula is P = 2l + 2w or P = 2(l + w).
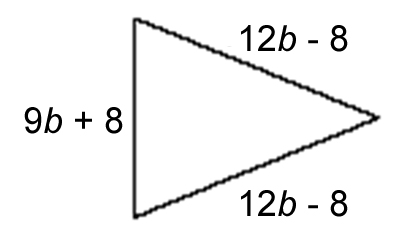
Let's try another one!
Lisa is making a banner in the shape of a triangle. She wants to line the banner with a decorative border. How long will the border be?