What are Significant Figures?
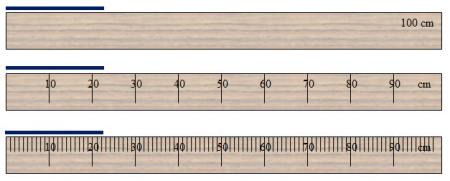
Above are three meter sticks broken down into different units: 1 meter, 10 units of 10 centimeters each, and 1-centimeter segments. The most precise measurement that can be made with the first stick is 1 meter. The second stick has a precision of 10 centimeters, and finally, the last stick has a precision of 1 centimeter.
If the first meter stick is used to measure the length of the blue line, an accurate reading cannot be made because the length is less than 100 cm. By using the second stick, an approximate guess can be made that the length is over 20 cm. Finally, the third meter stick shows that the length of the blue line is about 22 centimeters.
In scientific work higher precision levels are needed. Scientists express the level of precision by using significant figures. Let’s zoom in on the ruler and measure the object again.
Now that you have a better view of the object and ruler, you can see that the object is 22.5cm.
22.5 cm is a more precise number than the measurements that were taken before. The precision of the measurement 22.5 cm is 3 significant digits. When you are working out mathematical or scientific problems, you will need to know what level of precision or significant digits your answer should have. Significant figures of a number are the digits that contribute the precision of the number.
Because measurement requires human involvement, no measurement is exact. Measurements should include all accurately measured values and one uncertain digit (the last digit).
Significant Figure Rules
Like most things in science, significant figures have rules.
- Non-zero digits and zeros between non-zero digits are always significant.
- Leading zeros are not significant.
- Zeros to the right of all non-zero digits are only significant if a decimal point is shown.
- For values written in scientific notation, the digits in the coefficient are significant.
- In a common logarithm, there are as many digits after the decimal point as there are significant figures in the original number.
Let’s look at these rules one at a time and see some examples.
Rule 1: Non-zero digits and zeros between non-zero digits are always significant.
This rule has two parts. Let’s look at each part.
Part A: Non-zero digits are always significant.
This is the easiest rule. This rule simply means that all numbers that are not zero (1, 2, 3, 4, 5, 6, 7, 8, and 9) are always significant. The number 56.7 has 3 significant digits.
Part B: Zeros between non-zero digits are always significant.
If a zero falls between two non-zero numbers, it is significant. If you had a measurement of 805.74, you know 8, 5, 7, and 4 are significant based on Part A of Rule 1. The zero is also significant because it falls between two non-zero digits. So, 805.74 would have 5 significant figures.
Rule 2: Leading zeros are not significant.
Leading zeros are zeros that are “place holders.” The number 0.69 has a leading zero in the ones place. The 6 and the 9 are significant. So, 0.69 has two significant figures. The measurement .000156 nm has three significant figures.
Rule 3: Zeros to the right of all non-zero digits are only significant if a decimal point is shown.
These zeros are sometimes called trailing zeros because they come after (or to the right of) non-zero numbers. There are three different scenarios with trailing digits.
Scenario 1
There are trailing zeros in a whole number, and there is no decimal present.
When there are trailing zeros in a whole number, and there is not a decimal, these zeros are not significant. An example of this would be the measurement 5900000 grams. Since there is no decimal point in this measurement, there would be only two significant figures, the 5, and the 9.
Scenario 2
There are trailing zeros to the right of the decimal.
Trailing zeros to the right of a decimal are significant. An example of this would be the measurement 165.00 mL. In this measurement, the two trailing zeros are significant because there is a decimal shown.
Scenario 3
There are trailing zeros in a whole number, and there is a decimal present.
If there are trailing zeros in a whole number, and there is a decimal shown, then the zeros are significant. For example, the measurement 750. grams would have three significant zeros because of the decimal.
Rule 4: For values written in scientific notation, the digits in the coefficients are significant.
Scientific notation was discussed in the previous lesson of this module. Remember, a number expressed in scientific notation has two parts: the coefficient and 10 raised to a power. The measurement 6.40 × 10-3 moles would have three significant figures.
Rule 5: In a common logarithm, there are as many digits after the decimal point as there are significant figures in the original number.
A logarithm has two parts that are separated by a decimal. The digits before (to the left of) the decimal are called the characteristic, and the digits after (to the right of) the decimal are the mantissa. According to Rule 5, there should be as many digits in the mantissa as there are significant figures in the original number. Let’s look at an example.
log(2.43 × 101) has three significant digits. When you calculate the logarithm, you will get the following:
1.386
Notice that the original number had three significant figures and there are three digits in the mantissa. Since only the numbers in the mantissa are significant, this value only has three significant figures.
Rules Review!
Watch this video to review the rules of significant figures that deal with zeros.
Source: Significant Figures and Zero, Tyler DeWitt, YouTube
Calculations and Significant Figures
When making calculations in science, it is important to express the answer with the correct number of significant figures. In this section, you will look at the rules for calculations and significant figures.
Addition and Subtraction with Significant Figures
The rule for addition and subtraction with significant figures is as follows:
When measurements are added or subtracted, the final answer can contain no more decimal places than the least accurate measurement.
When adding and subtracting measurements, the level of accuracy at which you express your final answer does not depend on the number of significant figures in the original problem but instead is determined by the position or place value of the least significant digit in the original problem.
Watch the following video to see examples of adding and subtracting with significant figures.
Source: Add and Subtract With Significant Figures, Tyler DeWitt, YouTube
Now you try! Remember,
- complete the calculation as you normally would, and
- express the final answer by rounding to the place value corresponding to the number in the original problem with the least accurate place value.
Multiplication and Division with Significant Figures
The rule for multiplication and division with significant figures is as follows:
When measurements are multiplied or divided, the answer can contain no more significant figures than the least accurate measurement.
This rule simply means the final answer can be no more accurate than the least accurate measurement. Count the significant figures in each measurement instead of the number of decimal places when multiplying and dividing measurements.
Watch the following video to learn more about multiplying and dividing with significant figures.
Source: Multiplication and Division With Significant Figures, Tyler DeWitt, YouTube
Now you try! Remember,
- perform the calculation,
- count the number of significant figures in each measurement, and
- round the final answer using the least number of significant digits from the original problem.