Introduction
 More often than not, problems involving math appear as word problems instead of an equation or expression. In order to solve meaningful real-world problems, you need to be able to translate a word problem into a mathematical expression or equation. In this lesson, you will examine a variety of ways that you can do just that.
More often than not, problems involving math appear as word problems instead of an equation or expression. In order to solve meaningful real-world problems, you need to be able to translate a word problem into a mathematical expression or equation. In this lesson, you will examine a variety of ways that you can do just that.
One thing to keep in mind is the order of operations, which you have learned in previous grades.
Use the acronym PEMDAS to remind yourself about the order of operations.

In this lesson, you will focus on applying operations, including the order of operations, to solve real-world problems. You will also perform those operations on both positive and negative numbers and justify the selection of a given operation.

Identifying Operations from Problem Situations
 Sheila and her family are driving from Beaumont to west Texas to visit family. They will drive along Interstate 10.
Sheila and her family are driving from Beaumont to west Texas to visit family. They will drive along Interstate 10.
Sheila uses a road map to identify the mile markers for certain towns along the route. Those towns are shown on the map below.
Review the name of each city and the mile marker used along the highway for that city. You will use this information to answer the questions that follow.
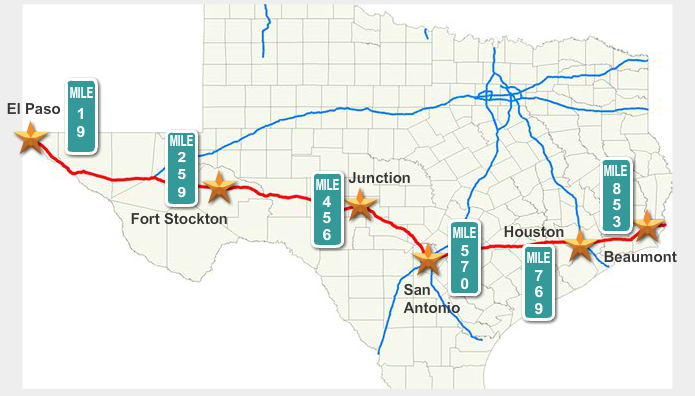
Use the information from the interactive activity to answer these questions. The formula d = rt, where d represents the distance, r represents the rate or speed of travel, and t represents the amount of time traveled, may be helpful.
Pause and Reflect
1. How can you tell which operation you need to perform in a problem?
2. What actions indicate addition?
3. What actions indicate subtraction?
4. What actions indicate multiplication?
5. What actions indicate division?
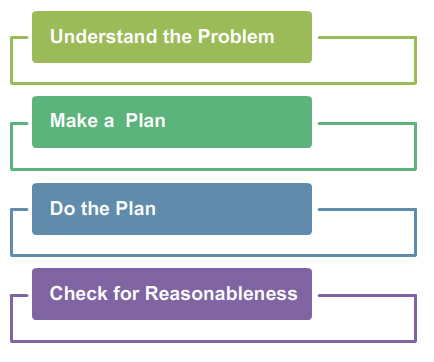
Formulating a Plan to Solve Problems
You have used what you know about addition, subtraction, multiplication, and division in order to write mathematical expressions from verbal problem situations. In this section, you will use that skill as part of the four-step problem-solving model.
 Armando received a new media player for his birthday. His favorite website allows him to download songs for \($\)0.95 each and movies for \($\)9.95 each. He downloaded 20 songs and some movies, earned a 20% discount, and his bill for the transaction was \($\)62.96 without sales tax. How many movies did Armando download? Justify your solution.
Armando received a new media player for his birthday. His favorite website allows him to download songs for \($\)0.95 each and movies for \($\)9.95 each. He downloaded 20 songs and some movies, earned a 20% discount, and his bill for the transaction was \($\)62.96 without sales tax. How many movies did Armando download? Justify your solution.
Use the problem solving model to solve Armando’s problem. For each section of the problem-solving model, select one of the two options (Option 1 or Option 2) by clicking on the answer choice that you think is best. Enlarge the image by clicking the plus sign.
Pause and Reflect
1. How can writing an expression or equation help you make a plan when solving problems?
2. Why is it important to always check your answer for reasonableness?
Practice Problems
Use the problem situation below to answer questions 1–4.
Madison is building a rectangular pen for her pet goat. The goat has a house that is a square with side lengths of 3 feet. The pen will have dimensions of 9 1/2 feet by 7.25 feet. What will be the area inside the pen and outside the house?
Justifying Your Choice of Operations
 You have investigated how to translate a word problem into mathematical operations and how to use the 4-step problem solving model. Now, you will focus on justifying an operation that you, or a student like you, have selected in order to solve a problem.
You have investigated how to translate a word problem into mathematical operations and how to use the 4-step problem solving model. Now, you will focus on justifying an operation that you, or a student like you, have selected in order to solve a problem.
For each problem below, Jaime needs to select an operation and write an expression to solve the problem. You will help Jaime by selecting the correct operation and expression.
Use your results from the interactive to answer the following questions.
- How does the order of the actions being performed in the problem affect the order of the operations that you select?
- If you need to add or subtract before multiplying or dividing, how can you override the order of operations, which tell you to multiply or divide before adding or subtracting?
Summary
Solving problems with rational numbers may require you to do a lot of work before you can actually solve the problem.
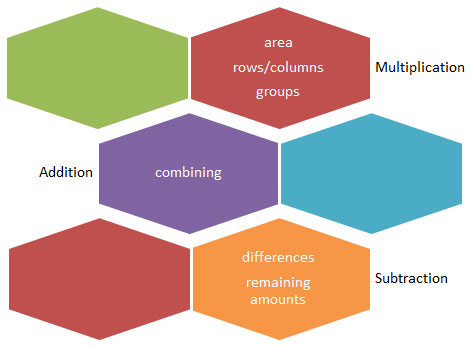
- You will need to identify the operations from the problem by the actions being performed in the problem.
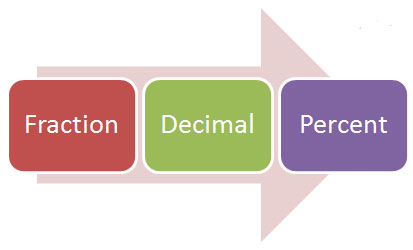
- You may need to convert rational numbers to an equivalent form.
- You may need to use a problem-solving plan.
