Proportional Relationships
This resource is about proportional relationships. To get started, read the following problem.

 |
A group of kids are making lemonade to sell at their lemonade stand. Following the recipe, they use 6 lemons and make 8 cups of lemonade. The next week, they use the same recipe with 9 lemons and make 12 cups of lemonade. |
 |
Sources of images used for this section:
Little boy, Microsoft clipart, office.com
Lemon tree - Korfu Zitronen, Jean-Luc 2005, Wikimedia commons
Glass of lemonade - Shekanjbeen, Mainsari66, Wikimedia Commons
Copy the following table into your notes, and use the information from the problem to fill in the empty cells.
|
Lemons
|
Cups of Lemonade
|
|
3
|
|
|
6
|
8
|
|
9
|
12
|
|
12
|
|
|
15
|
|
Click here to see the completed table.
Use the table to answer the following questions.
1. What happens to the amount of lemonade the recipe makes if you double the number of lemons?
2. What happens to the amount of lemonade the recipe makes if you triple the number of lemons?
3. What happens to the amount of lemonade the recipe makes if you change the number of lemons by any scale factor?
4. What rule did you use to fill out the missing information?
The kids decide to sell lemonade one more time. When they go to the fruit bowl they find that they have 5 lemons. How much lemonade can they make now?
|
Lemons
|
Cups of Lemonade
|
|
3
|
4
|
|
5
|
?
|
|
6
|
8
|
|
9
|
12
|
|
12
|
16
|
|
15
|
20
|
Solve the problem on a separate piece of paper, then watch the video to check your answer.
Answer the following questions based on what you saw in the video.
- What was the scale factor used in the first method of solving the problem?
Check Your Answer - What did this scale factor mean?
Check Your Answer - What was the constant of proportionality used in the second method of solving the problem?
Check Your Answer - What did this constant of proportionality mean?
Check Your Answer
 This problem required proportional reasoning. Whatever factor you use to change one variable—in this case, the number of lemons, you also use that factor to change the other variable—the number of cups of lemonade.
This problem required proportional reasoning. Whatever factor you use to change one variable—in this case, the number of lemons, you also use that factor to change the other variable—the number of cups of lemonade.
Danny is helping to decorate the gym for a school dance. It takes Danny 10 minutes to hang 4 strings of flashing lights. If Danny continues to work at the same pace how long will it take him to hang 7 strings of lights?
Source: Platonic solids Lantern, The Playful Geometer, Flickr
Copy the following table into your notes, and fill it in with the values from the problem.
| Strings | Minutes |
|---|---|
Click here to see the completed table.
Answer the following questions based on the information in the table.
Proportions
One way that we can represent problem situations in math is by writing equations.
Proportional relationships are often written as an equation that shows two ratios—written as fractions—equal to each other.
The ratios either show the scale factor used to change one number to another, or the ratios show the constant of proportionality. In the video example in section 1, the first method shows how to use a scale factor to change from 3 lemons to 5 lemons. The video also shows a second method: using the constant of proportionality that tells you how 1 lemon can be used to make cup of lemonade.
The numbers from your data table will fill in the boxes in a proportion like this:
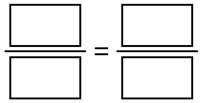
Here is an example.

Source: Question book-2, AzaToth, Wikimedia Commons
A good first step is to enter all the information from the problem into a table like this one:

| pages | minutes |
Source: Stopwatch2, Hydragyrum,
Wikimedia Commons
Copy the table into your notes, and then fill in the given information.
The following video animation will place the numbers from the data table into the equation.
Now you try one.
An architect is building a house based on a special scaled diagram called a blueprint. A 2-inch line segment in the diagram represents a 10-foot wall in the actual house. What length line segment would be used to represent a 17-foot wall?
1. What are two things that are being compared to each other?
2. What changes from one wall to the other?
Copy the following table into your notes.
| length of wall | length of line segment | |
| Wall 1 | ||
| Wall 2 | ||
Fill in the empty spaces in the table with information from the problem.
How you could use the data from the problem (10, 2, L, 17) to fill in the proportional equation?
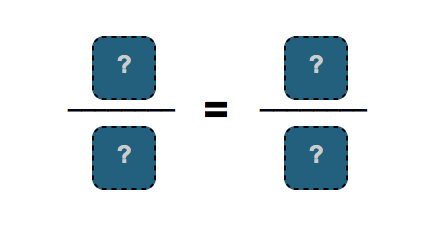
Solve your equation for L on a separate piece of paper.
Practice
Here are three examples for you to try on your own. If you get stuck, click on the hint buttons. Following each example are samples of four multiple choice options.