Review of Dimensional Analysis, Scientific Notation, and Significant Figures
When you are performing mole conversion problems, it is important to remember how to perform dimensional analysis and the rules for significant figures. Often, you will need to express your answers in scientific notation. Let’s briefly review each of these skills.
Dimensional Analysis
- Dimensional analysis, or the factor label method, is a useful problem-solving technique that can be used to convert between units.
- Dimensional analysis uses conversion factors, or equivalences, set up in a manner that allows “like” units to cancel one another.
- When solving problems using dimensional analysis
- always start with the given information, and then
- set up a conversion factor with the original unit in the denominator and the new unit in the numerator.
Remember the STAAR reference material for Chemistry has a section titled Constants and Conversions. Refer to this as you work various problems.

Source: STAAR Reference Material, Texas Education Agency
Listed below are some other common unit conversions as well as common metric prefixes used in science.
Write the given information as a fraction by placing it over 1. (Placing it over 1 makes it a fraction but does not change its value.)
- Write a conversion factor that has the unit you want to remove in the denominator and the unit you want to end up with in the numerator. After you fill in your units, add the numbers. (Usually one of the numbers is a 1, but it can be in either the denominator or the numerator.) Note: In some cases you may need to repeat this step a number of times in order to get the unit you want to end up with in the numerator.
- Mark through the units to double check that they all cancel and that you are left with the units you want.
- Multiply the numbers in the numerators, and then multiply the numbers in the denominators.
- Divide the numerator by the denominator. Be sure to add your units to your final answer.
Scientific Notation
- Scientific notation expresses very large or small numbers in a simplified manner.
- In scientific notation, a number is written as the product of two numbers: a coefficient and 10 raised to a power.
- Example 1: 6500000000 can be written in a simpler way: 6.5 × 109
- Example 2: 0.000000042 can be written in a simpler way: 4.2 × 10-8
- Numbers with positive exponents are large numbers.
- Numbers with negative exponents are small numbers.
- To write numbers using scientific notation, move the decimal, and write the number of places you moved the decimal point as an exponent.
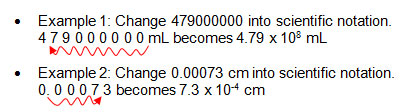
Significant Figures
The STAAR reference material for Chemistry document lists the rules for significant figure in a section titled Rules For Significant Figures.
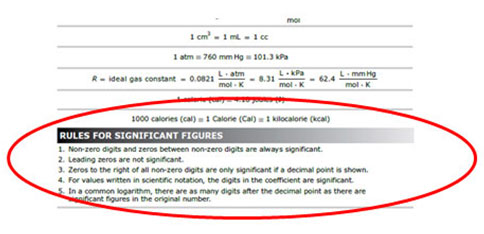
Source: STAAR Reference Material, Texas Education Agency
The rule for addition and subtraction with significant figures is as follows:
When measurements are added or subtracted, the final answer can contain no more decimal places than the least accurate measurement.
When adding and subtracting measurements, the level of accuracy at which you express your final answer does not depend on the number of significant figures in the original problem but instead is determined by the position or place value of the least significant digit in the original problem.
The rule for multiplication and division with significant figures is as follows:
When measurements are multiplied or divided, the answer can contain no more significant figures than the least accurate measurement.
This rule simply means the final answer can be no more accurate than the least accurate measurement. Count the significant figures in each measurement instead of the number of decimal places when multiplying and dividing measurements.
