Introduction
Transforming polygons is an important application of coordinate geometry. Digitally-designed art, including graphics and video games, all rely on transformations of polygons in order to move figures and characters around the screen.
To perform a dilation on a coordinate plane, you need to know two pieces of information. First, you need to know the scale factor, or magnitude of the enlargement or reduction. Second, you need a center of dilation, or reference point from which the dilation is generated.
In this resource, you will investigate more properties of dilations.
Center of Dilation Inside the Figure
Use the interactive link shown below to investigate coordinate dilations. Once you have done so, use your experiences to answer the questions that follow.
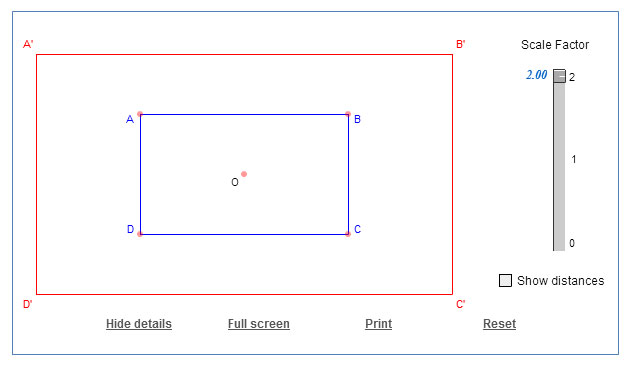
Use the interactive sketch below to dilate the quadrilateral ABCD. Initially, you will see rectangle ABCD, but you can change the shape of the quadrilateral by dragging the orange dot representing each vertex of the figure. Use the slider to change the scale factor of dilation.
Click to see additional instructions in using the interactive sketch.
Click on the image below to access the interactive.
Use the slider to adjust the scale factor.
- What types of scale factor will generate a reduction?
- What types of scale factor will generate an enlargement?
Use the same interactive sketch to complete the following table. Reset the sketch and make sure that the “Show distances” check box is selected.
Make a copy of the table, and paste it into your notes. Fill in the columns for Length of OB and Length of OB' . Use the slider to adjust the scale factor while you keep the length of OB the same.
| Length of OB | Scale Factor | Length of OB' |
| 0.5 | ||
| 0.7 | ||
| 1.2 | ||
| 1.4 | ||
| 1.75 | ||
| 2 |
Use the data in your table to answer the questions that follow.
- How does the length of OB' compare to the length of OB and the scale factor?
- What does the length of OB tell you about the distance between the center of dilation and Point B?
- What does the length of OB' tell you about the distance between the center of dilation and Point B'?
- How does the scale factor affect the distance between a point in a polygon and the distance from the center of dilation?
- Change the shape of quadrilateral ABCD by clicking and dragging Point B to move it. Is the relationship you just observed true for other polygons as well?
Center of Dilation Outside the Figure
Use the same interactive sketch to complete the following table. Reset the sketch and make sure that the “Show distances” check box is selected. Move the center of dilation, Point O, outside of rectangle ABCD.
For example, you could move Point O above and to the right of Point B.
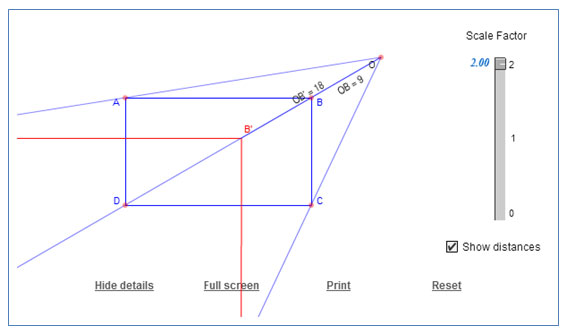
Make a copy of the table, and paste it into your notes. Fill in the columns for Length of OB and Length of OB'. Use the slider to adjust the scale factor while you keep the length of OB the same.
| Length of OB | Scale Factor | Length of OB' |
| 0.5 | ||
| 0.7 | ||
| 1.3 | ||
| 1.4 | ||
| 1.8 | ||
| 2 |
Use the data in your table to answer the questions that follow.
- How does the length of OB' compare to the length of OB and the scale factor?
- Does the location of the center of dilation, with respect to the polygon being dilated, change the relationship you observed before between the scale factor and the distance between a point in a polygon and the center of dilation?
- Change the shape of quadrilateral ABCD by clicking and dragging Point B to move it. Is the relationship you just observed true for other polygons as well?
- Click and move the slider to change the scale factor. How does the location of Point C' compare to ray OC, created by starting with Point O and extending a part of a line through Point C
Applying Coordinate Dilations
A common application of coordinate dilations is displaying digital images on a computer monitor.
A computer monitor, or computer screen, contains a certain amount of pixels. A pixel is a point on the monitor that lights up with a particular color, depending on the program that is being run.
 Pixels are given a location using Quadrant I of a coordinate plane. Computer programs use x- and y-coordinates to locate each pixel and assign it a particular color.
Pixels are given a location using Quadrant I of a coordinate plane. Computer programs use x- and y-coordinates to locate each pixel and assign it a particular color.
For example, the monitor shown in the picture has a horizontal dimension of 1366 pixels and a vertical dimension of 768 pixels. Each pixel on the monitor can be used to generate an image.
The pixel shown is 1200 pixels from the left-hand corner, or origin, and 721 pixels above the left-hand corner, or origin. It is the pixel located at the ordered pair (1200, 721).
Let’s see this in action. Adan is a computer programmer, and he wants to generate an animation sequence by enlarging a figure whose outline is the trapezoid shown on the graph below. He is using a computer monitor like the one shown before, with a horizontal dimension of 1366 pixels and a vertical dimension of 768 pixels. His computer screen and the outline of the image are shown on the graph below.
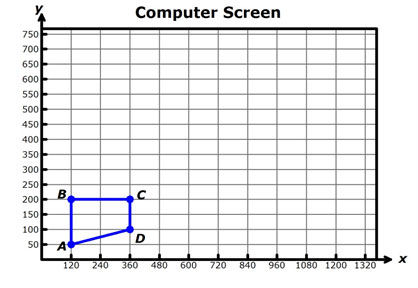
First, let's practice with the following activity using scale factors to identify new coordinates. The slider on the left hand side changes the scale factor.
Use the information from the graph to fill in the chart below.
|
|
|
|||||
|
Point |
Original Coordinates |
Scale factor |
Scale factor 1.5 |
Scale factor |
Scale factor |
Scale factor |
|
A |
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
Study the table you created. Describe how the scale factor can be used to determine the new coordinates.
Now that you practiced finding the coordinates using scale factors, go back to the graph showing the outline of the image Adan would like to enlarge.
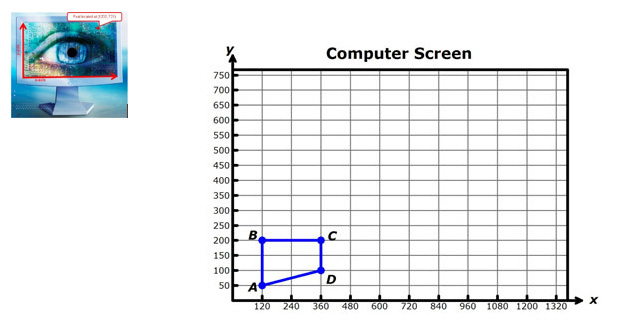
Copy the table below in your notes, and fill in the blanks.
|
|
New Coordinates |
||||
|
Point |
Original Coordinates |
Scale factor |
Scale factor |
Scale factor |
Scale factor |
|
A |
(120,50) |
|
|
|
|
|
B |
(120,200) |
|
|
|
|
|
C |
(360,200) |
|
|
|
|
|
D |
(360,100) |
|
|
|
|
Practice
Pentagon ABCDE is the outline of a figure on a computer screen. The pixels representing the vertices of the pentagon are shown below.
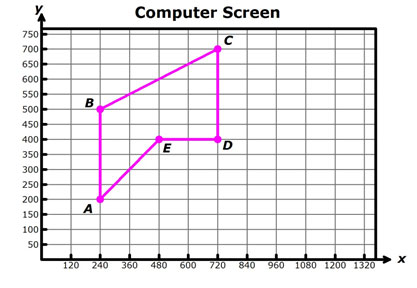
- If the figure is dilated by a scale factor of 0.6, what will be the coordinates of each new pixel?
2. If the original figure is dilated by a scale factor of , what will be the coordinates of each new pixel?
Hexagon ABCDEF is the outline of a figure on a computer screen. The pixels representing the vertices of the pentagon are shown below.
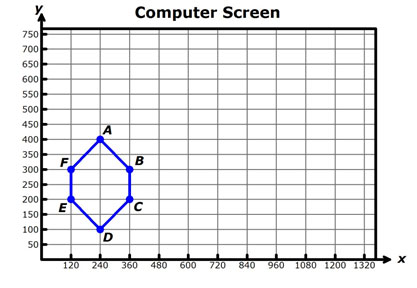
3. If the original figure is dilated by a scale factor of , what will be the coordinates of each new pixel?
4. Beatrix, the computer programmer, wants to dilate the figure using a scale factor of 225%. If she does, will the image still fit on the computer screen with dimensions of 1366 pixels by 768 pixels? How can you tell?
Summary
Coordinate dilations are important for several reasons.

Computer programmers and graphics designers use coordinate dilations to animate and design digital images on the computer screen.

Structural engineers and draftsmen use dilations to generate images with computer-assisted design software in order to construct useful objects.
You can also use dilations to enlarge or reduce graphs of data.
Regardless of the application, enlargements and reductions of figures represented on the coordinate plane can be very useful and help you solve meaningful, real-world problems.