Introduction
Similar figures are polygons or other figures that are proportional in shape.
When you have similar figures, you have learned in previous grades that two things are true.

In this lesson, you will extend what you know about similar figures to dilations. A dilation is an enlargement or reduction of a figure by a given scale factor.
Generating Similar Figures Using Dilations
In this section, you will use dilations in order to generate similar figures.
Use the Generating Similar Figures Using Dilations interactive to dilate ΔABC. Click and drag on the slider to dilate ΔABC to create ΔDEF. The number on the slider indicates the scale factor used to generate the dilation. Use the interactive to complete the table that follows. Use the table to answer the questions after the table.
Copy and paste the table below to your notes, or a word processing document, to enter your data.
|
Scale Factor (f)
|
|
|
|
|
0.25
|
|||
|
0.75
|
|||
|
2
|
|||
|
2.5
|
- How does the ratio of the lengths of each pair of corresponding sides compare for a dilation generated using a given scale factor?
- If two or more ratios are equal, what does that tell you about the lengths of the corresponding sides?
- How does a dilation compare to a pair of similar figures?
Pause and Reflect
In the interactive, you used a dilation to generate a pair of similar triangles. Do you think the same relationship would hold true if you dilated a quadrilateral? Why or why not?
Writing Proportions from Dilations

In the last section, you investigated how a dilation is used to generate a new figure (image) from an original figure (pre-image). You also saw that the ratios of any pairs of corresponding sides from the dilation were equal. That means the lengths of corresponding sides are proportional, which is one of the attributes of similar figures.
Now that you’ve seen how dilations can be used to generate similar figures, you can use dilations to set up and solve proportions.
Consider the dilation shown below. Trapezoid JKLM is generated by dilating trapezoid ABCD.
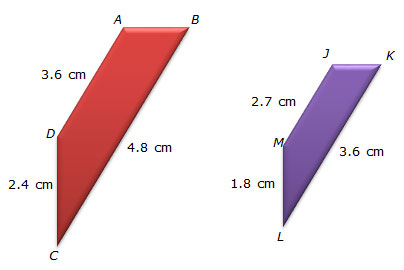
- How can you identify a pair of corresponding sides?
- Once you have identified two pairs of corresponding sides, how can you use that information to write a proportion?
Use the link to complete the interactive activity.
Example 1: Solve the proportion for x.
- Find the scale factor. In this example the scale factor is 4 (3 × 4 = 12).
- Multiply by the scale factor.
- Since x is in the denominator, find the denominator. x = 8(4) = 32
x = 32
Example 2: Solve the proportion for x.
- Find the scale factor. In this example the scale factor is 3 (7 × 3 = 21).
- Multiply by the scale factor.
- Since x is in the numerator, find the numerator. x = 2(3) = 6
x = 6
Pause and Reflect
Once you have the proportion written, how could you solve the proportion?
Summary
In this lesson, you applied what you have previously learned about similar figures to dilations. A dilation is when you generate a second figure from an original figure with a particular scale factor. Because the corresponding sides of both the dilated figure and the original figure are proportional, the two figures are similar.
In the figure below, ΔFGH is generated by dilating ΔABC by a scale factor of 2.
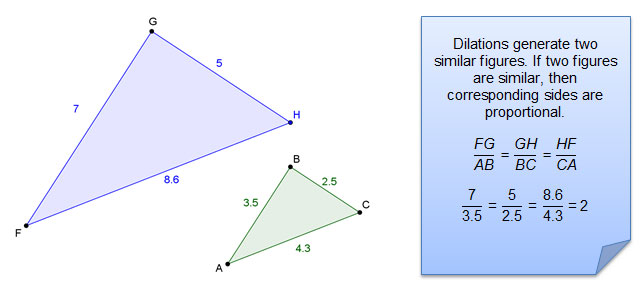
Complete the following proportion:
Use the information above and angle congruence to complete the proportion.
- Side OP corresponds to ∠O and ∠P.
- ∠C and ∠D are congruent to ∠O and ∠P.
- The side missing in the proportion is CD.