Introduction
You’ve used probability to describe the likelihood of events occurring. In this lesson, you will investigate how you can calculate the probability of two or more events.
Probability is used to describe how likely something is to happen. For example, you may have heard the weather forecaster describe the chances that it will rain today. She is using probability to make that forecast.
Probability is formally defined as the ratio of the number of desired outcomes (what you want to happen) to the number of total possible outcomes (what could possibly happen). Probability is a ratio, so it can be expressed as a fraction, a decimal, or a percent.


The probability of rain today is 80%. That means that there is an 80% chance that the event of rain will occur.

Out of a dozen dyed eggs, there are 2 blue ones. The probability of randomly choosing a blue egg is . Since this is only one event occurring, this is called a simple event.

There is a 7 out of 10 chance that someone will catch the flu if they don't get a flu shot. The probability of getting the flu is 0.7.
Determining the Probability of Independent Events
 The relationship between multiple events that occur is important. Sometimes, when an event occurs, it does not affect the chances of the next event(s) occurring. For example, when you roll a pair of number cubes, the number that lands on the top face of one number cube does not affect the number that lands on the top of the second number cube.
The relationship between multiple events that occur is important. Sometimes, when an event occurs, it does not affect the chances of the next event(s) occurring. For example, when you roll a pair of number cubes, the number that lands on the top face of one number cube does not affect the number that lands on the top of the second number cube.
When there is an independent relationship between two or more events, those events are called independent events.
Consider the spinner shown.
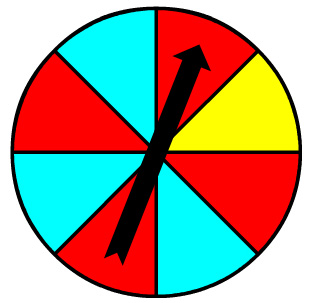
Use the image of the spinner to determine the probability of the spinner landing on red, aqua, or yellow.
The probabilities that you just identified are for the simple event of the spinner being spun once. Suppose, however, that the spinner is spun twice. Because two simple events will occur, these events become compound events.
You will also notice that the outcomes of these compound events (the spinner being spun twice) are not related to each other. That is, the results of the second spin do not depend on the results of the first spin. Since that is the case, we can call these events independent events.
To determine the probability of a set of independent events, we must first identify the probabilities of each of the events occurring by themselves.

Three friends are using the spinner to play a board game. Drag the fraction that represents the probability of each of the following events to the space indicated. For example, for the first line, drag the fraction representing the probability of the spinner landing on yellow to the box in the Probability of First Event column. Drag the fraction representing the probability of the spinner landing on red to the box in the Probability of Second Event column.
Now, calculate the probability of both events occurring for each player by multiplying the probability of the first event and second event together.
 Hot Tip!
Hot Tip!
The principle that allows us to calculate the probability of two or more events occurring is also called the Multiplication Rule and is written as follows:
P(A and B) = P(A) x P(B)
We are also often interested in the probabilities of events resulting from a drawing. If something is drawn, replaced, and then drawn again, the events are independent. This means that the outcome of the second drawing does not depend on the outcome of the first drawing.
Mr. Aimone wrote the names of eight students on slips of paper. He uses the paper slips to randomly draw a student's name to answer questions in his class. After each drawing, Mr. Aimone replaces the slip so that there are always eight slips in the bag. The names of the eight students are as follows:
|
Brandon |
Chita |
Khambrel |
Courtney |
|
Monica |
Thao |
Kelsey |
Ahmed |
Determining the Probability of Dependent Events
Sometimes, when you have a series of compound events, the outcome of the first event does affect the outcomes of the subsequent events. These events are called dependent events since the outcome of the second (or third) event depends on the outcome of the first event.
Suppose a bag contains several color tiles: 6 red tiles, 4 green tiles, 3 yellow tiles, and 2 blue tiles.

Ramona reaches into the bag without looking and randomly pulls out one color tile. Use the bag containing the tiles to determine the probability of each color being drawn.
The probabilities that you just identified are for the simple event of one color tile being drawn. Suppose, however, that Ramona draws two tiles at the same time. Because two simple events will occur, these events become compound events.
However, unlike the spinner in the previous section of the lesson, the outcomes of these compound events (two color tiles being drawn at the same time) are dependent on each other. That is, the results of the second tile that is drawn depend on the results of what happened when the first tile was drawn. Since that is the case, we can call these events dependent events.
To determine the probability of a set of dependent events, we must first identify the probabilities of each of the events occurring by themselves. However, the circumstances describing the second event depend on what happened the first time.
In the case of drawing objects, once the first tile has been selected, there are fewer possible outcomes for the second tile (one less). So, we must reduce the denominator in the probability of the second tile by one.

Ramona will draw two tiles from the bag at the same time. Drag the fraction that represents the probability of each of the following events to the space indicated. For example, for the first line, drag the fraction representing the probability of Ramona drawing a red tile first to the box in the Probability of First Event column. Drag the fraction representing the probability of Ramona drawing a green tile second to the box in the Probability of Second Event column.
Hint: The number of tiles left after the first tile has been selected has decreased by one.
Now, calculate the probability of both events occurring for each player by multiplying the probability of the first event and second event together.
Click here to check your answer.
 Hot Tip!
Hot Tip!
You will also see the words “without replacement” in problems involving the drawing of two objects. This phrase is a clue that you have a situation with dependent events.
Practice
 Ms. Dawson’s 1st period science class has 18 girls and 12 boys. Ms. Dawson needs to select a pair of students to help her set up a laboratory investigation. She has decided to randomly select 2 students from the entire class.
Ms. Dawson’s 1st period science class has 18 girls and 12 boys. Ms. Dawson needs to select a pair of students to help her set up a laboratory investigation. She has decided to randomly select 2 students from the entire class.
Determining Probability—“And” versus “Or”
In the previous two sections, you have investigated situations where two events took place. What happens to the probability if we are only concerned about whether or not a combination of choices could happen? As long as these choices could not happen together, they are called mutually exclusive events. There are shortcuts for determining the probability of these events.
Consider the spinner shown.
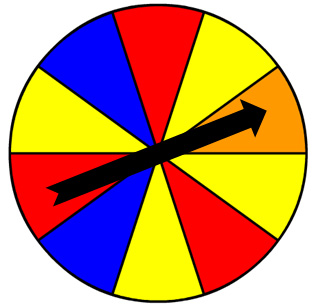
Use the spinner to determine the probability of the spinner landing on red, blue, yellow, or orange.
The probabilities that you just identified are for the simple event of the spinner being spun once. Suppose, however, that the spinner is spun twice. Because two simple events will occur, these events become compound events.
To determine the probability of a set of mutually exclusive events, we must first identify the probabilities of each of the events occurring by themselves.

Three friends are using the spinner to play a board game. Drag the fraction that represents the probability of each of the following events to the space indicated. For example, for the first line, drag the fraction representing the probability of the spinner landing on yellow to the box in the Probability of First Event column. Drag the fraction representing the probability of the spinner landing on red to the box in the Probability of Second Event column.
Now, calculate the probability of both events occurring for each player by adding the probability of the first event and second event together.
 Hot Tip!
Hot Tip!
The principle that allows us to calculate the probability of two or more mutually exclusive events occurring is also called the Addition Rule and is written as follows:
P(A or B) = P(A) + P(B)
Practice
Brandy and her sister are playing a card memory game. Brandy wrote the letters shown on index cards.

Brandy will turn the cards over and shuffle them, then randomly draw a card from the pile.
Summary
In this lesson, you investigated different ways to compute the probability of two or more events occurring.
Mutually exclusive events are two or more events that cannot both happen at the same time. You can calculate the probability of a set of mutually exclusive events by using the Addition Rule of Probability as follows:
P(A or B) = P(A) + P(B)
Independent events are two or more events that occur in sequence where the outcome of the first event does not affect the outcome of the events that follow. You can calculate the probability of a series of independent events by using the Multiplication Rule of Probability as follows:
P(A and B) = P(A) × P(B)
Dependent events are two or more events that occur in sequence where the outcome of the first event does affect the outcome of the events that follow. You can calculate the probability of a series of dependent events by using the Multiplication Rule of Probability as follows:
P(A and B) = P(A) × P(B|A)
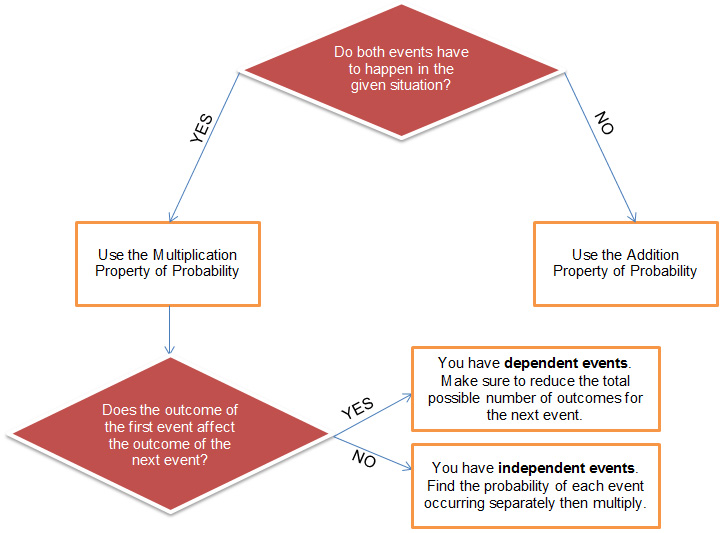
The flowchart shown can be used to help you determine how to approach different probability problems.