In math, we use an exponent as a short way of writing the same number multiplied by itself several times. For example: 3⁴ = 3 × 3 × 3 × 3, or 12⁵ = 12 × 12 × 12 × 12 × 12. The exponent tells you how many times the number (called the base) will be multiplied by itself.

Some numbers, like 2 and 10, make easy-to-solve patterns when repeatedly multiplied. The pattern for repeatedly multiplying by 2, for example, is to just keep doubling the result.

Copy and complete the following table on a separate piece of paper to find the pattern for 10.

Click here to see a completed table.

Based on the information in the table, answer the following questions in your notes:

1. How do the numbers in the bottom row change as you move from left to right?
2. How does the number of zeros in the final answer compare to the number of times 10 is used as a factor?
3. What rule does this suggest for how the number of zeros in the final answer compares to the exponent in the top row?
4. Using your rule, how would you write one billion (1,000,000,000) as 10 raised to an exponent?
5. What would happen if you raise 10 to no power? 10⁰ = ?

Positive exponents tell us how many times we multiply by a number. Negative exponents tell us how many times we divide by a number—or how many times we multiply by $\frac{1}{number}$.

Based on the two examples given above, fill in the following table.

Click here to see a completed table.

Based on the information in the table, answer the following questions in your notes.

1. What happens to the number in the bottom row as you move from left to right?
2. How does the number of zeros after the decimal compare to the number of times you use $\frac{1}{10}$ as a factor?
3. How does the decimal place where you write the 1 compare to the number of times you use $\frac{1}{10}$ as a factor?
4. What general rule can you use to tell where to write the 1 in the decimal based on the exponent?
5. Based on your rule, how do you write 0.00000001 as 10 raised to an exponent?

Click here to see a table of values for 10 raised to the powers of -6 to +6.

Some numbers we use are simply too large to efficiently write out. For example, the mass of the Earth is 5,980,000,000,000,000,000,000,000 kilograms. This is a really large number, and it may be difficult to keep track of all of the zeros.

Let’s learn a strategy that can help in situations like this.

Look at the following three examples:

30 = 3 x 10

600 = 6 x 100

800,000 = 8 x 100,000

Use what you observed to complete the two number sentences below.

What are we doing in each of these examples?

Watch the following video as it applies this fact and what we learned in section 1 to the number 7,560,000,000.

Scientific notation writes very large numbers as a coefficient times 10 raised to an exponent:

Coefficient x 10^exponent

When writing a number in scientific notation the coefficient must have a value that is greater than or equal to 1 and less than 10.

1. In the example in the video, what was the coefficient?
2. What was the exponent?

1. What exponent should we use to write the power of 10 for the mass of the earth?
2. What is the mass of the earth written in scientific notation?
3. How many places was the decimal point moved to convert to scientific notation?

Sometimes we are faced with numbers that are very large, but other times, we must work with numbers that are very small. For example, the mass of a dust particle is 0.000000000753 kilograms.

1. If the mass a dust particle is written in scientific notation, what will be the coefficient?
2. What is the first digit in the coefficient?
3. In which decimal place is that number?
4. From the rule that you generated in section 2 of this resource, how would you write 10 raised to a power so that it would equal a decimal that has a 1 in the 10th decimal place?
5. How would you write the mass of a dust particle in scientific notation?
6. How many places, and in what direction, was the decimal point moved to convert 0.000000000753 kilograms to scientific notation?

Important note: The negative sign means that this is a decimal between 0 and 1, it does not make the number itself negative. To write a negative number in scientific notation, you need to make the coefficient negative.

Watch the following video to review the rules of writing numbers in scientific notation.

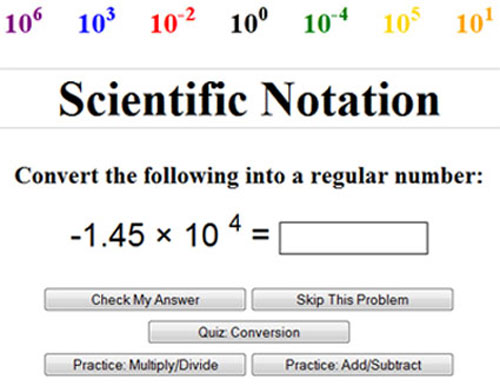
Click on the image below to access the applet. Enter numbers in the blank, and then click check my answer. Work through the applet until you get 10 correct.

The last thing we need to cover about numbers written in scientific notation is how to use them on a calculator. Watch the following video, and then answer the following questions.

1. What does a calculator use to display the "×10^exponent" part of a number written in scientific notation?
2. How do you enter the "×10^exponent" part of a number written in scientific notation?