Introduction
Probability describes the likelihood of an event, or a sequence of events, occurring.
People have been using numbers to describe how likely an event is to occur since at least early Greece and Egypt. In the 1650s, mathematicians Pierre de Fermat and Blaise Pascal wrote a series of letters to each other in which they discussed the mathematics of random events. Specifically, Fermat and Pascal wanted to describe the likelihood of certain outcomes including rolling number cubes, or dice, that were used to play popular games of their time.

Source: Blaise Pascal, GianniG46, Wikimedia Commons and Pierre de Fermat, Afernand74, Wikimedia Commons
In this lesson, you will investigate what Pascal and Fermat described in their letters almost 400 years ago. You will begin by investigating the probability of one event. This is called a simple event. Then, you will extend this idea to determine the probability of several independent events. Independent events are those whose outcomes do not affect other events. In a later lesson, you will compare the probability of independent events to the probability of dependent events, where the probability of any event does affect the outcome of other event(s).
Determining the Probability of Simple Events
Probability is defined as the ratio of the number of desired outcomes (what you want to happen) to the number of total possible outcomes (what could possibly happen). Probability is a ratio, so it can be expressed as a fraction, a decimal, or a percent.

 In probability, a simple event is one action or observation. For example, you could roll a six-sided number cube. An event in this situation would be a number landing face up on the number cube. Face up means the number that is showing on the top face of the number cube.
In probability, a simple event is one action or observation. For example, you could roll a six-sided number cube. An event in this situation would be a number landing face up on the number cube. Face up means the number that is showing on the top face of the number cube.
If each face is numbered with a digit from 1 through 6, what are the possible outcomes for rolling a number cube?

Use the six-sided number cube shown above to answer the following questions.
Pause and Reflect
- How can you determine the total number of outcomes for an event?
- How can you determine the number of desired outcomes for an event?
Practice
 Brianna and Desmond use an 8-sided die (which is not a cube, but an octahedron) to play a board game. Each face of the octahedron contains a digit from 1 to 8, and each face of the octahedron is congruent, so each number has an equal chance of appearing on the top face.
Brianna and Desmond use an 8-sided die (which is not a cube, but an octahedron) to play a board game. Each face of the octahedron contains a digit from 1 to 8, and each face of the octahedron is congruent, so each number has an equal chance of appearing on the top face.
Source: 4d8, Troumad, Wikimedia Commons
Determining the Probability of Independent Events
In the last section, you used fractions to write the probability of a simple event. In this section, you will extend that concept to determining the probability of a sequence of independent events occurring.

A bag contains 2 red tiles, 6 green tiles, 1 blue tile, and 3 yellow tiles. Match each simple event with the probability that the event will occur.
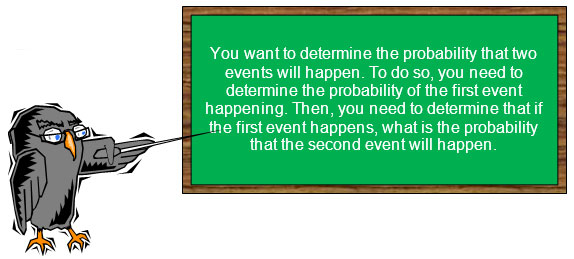
Suppose you want to determine the probability that Jeremy will randomly draw a blue tile, replace the tile, and then draw a yellow tile. Use a Venn diagram to represent the relationship between these two events.
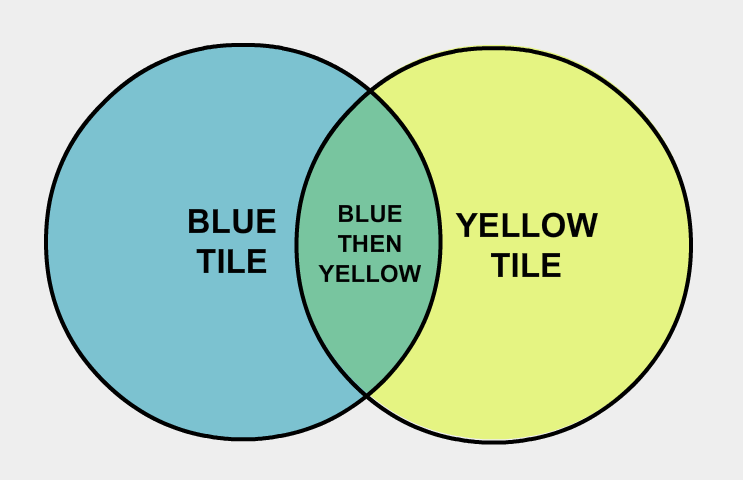
Pause and Reflect
What operation would you use to find the probability of an event in the intersection of this Venn Diagram?
Use what you have seen so far to answer the following questions.
Making Predictions from Data
In the previous sections, you examined ways to determine the probability of simple events and independent events. In this section, you will use data to make predictions from the probability of one or more events.

Sources: Cedar Hill State Park, QuesterMark, Flickr
San Jacinto Monument Star, Tijuana Brass, Wikimedia Commons
Big Tree, Larry D. Moore, Wikimedia Commons
Mustang State Park Nima, Zereshk, Wikimedia Commons
Garnerview3, Baylordad, Wikimedia Commons
A recent survey of Texas state park users revealed the five most popular state parks. The results are shown in the table below.
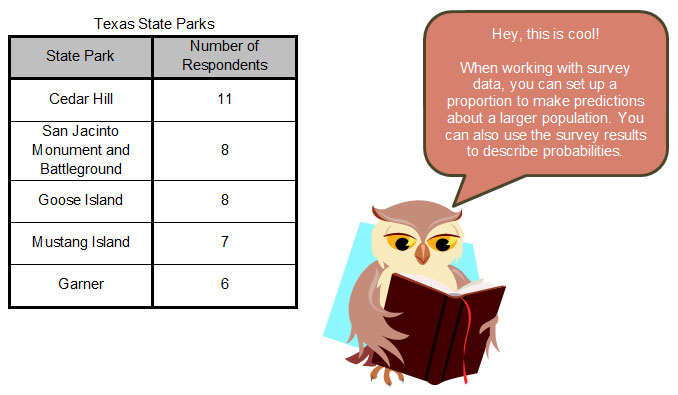
Use the data in the table to answer the following questions.
Pause and Reflect
How can you use data to determine the probability that an event will occur?
Practice
Majida surveyed 30 of her classmates to determine which sport was their favorite. Her results are shown in the table below. Use this information to answer the questions that follow.
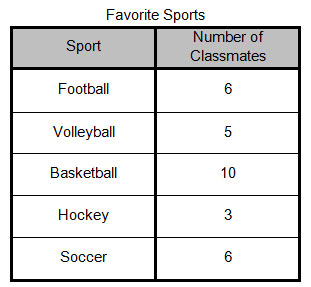
Summary
In this lesson, you investigated several different ways to use probability. Review the summary below.


