Introduction
Recall that similar figures have the same shape but not necessarily the same size. You can also generate similar figures using a scale factor.
Consider the two rectangles shown below.

The angles in Rectangle 1 are congruent to the corresponding angles in Rectangle 2. After all, a rectangle contains four right angles, and all right angles are congruent. However, the sides are not congruent. Let's take a closer look at the side lengths using proportions.
Since the ratios of the corresponding side lengths are proportional, we can say that the rectangles are similar.
We can also use the ratios of corresponding sides to identify the scale factor that is used to generate Rectangle 2 from Rectangle 1.

In this example, the scale factor is because the dimensions of Rectangle 1 are multiplied by to generate the dimensions of Rectangle 2.
How does this dilation affect the area of the new rectangle? You will investigate that relationship.
Determining Surface Areas of Prisms
One of the 3-dimensional figures you will explore is a prism. In this lesson, you will focus on triangular prisms and rectangular prisms. Recall that a prism is named by its congruent, parallel bases, so a triangular prism is a prism whose bases are triangles.
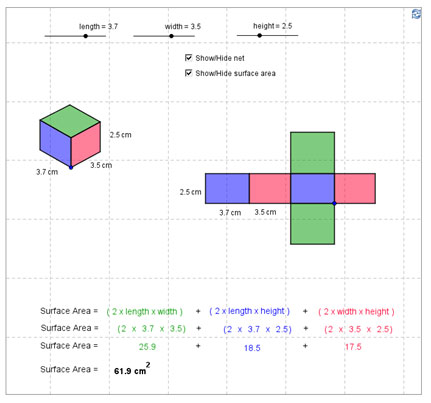
The Sparklee Jewelry Store is making small boxes in the shapes of rectangular prisms. The bases of each box will be green, and the lateral faces will be purple and red.
Use the activity below the following table to complete the table. Copy the table into your notes and record your answers.
| Length | Width | Height | Lateral Surface Area |
Total Surface Area |
| 2.5 cm | 3.5 cm | 2 cm | ||
| 3.5 cm | 3.5 cm | 2 cm | ||
| 4 cm | 2.5 cm | 2.5 cm | ||
| 3 cm | 3.5 cm | 4.5 cm |
Click on the image below to access the interactive. Scroll down the page to see the Geogebra applet.
Click here for directions on how to use the applet.
Triangular Prisms
Sparklee Jewelry Store is also creating boxes in the shapes of right triangular prisms.
In the activity below, drag the dimensions to the appropriate place in the formula to calculate the lateral surface area of the box.
Now that you have correctly identified the dimensions, calculate the lateral surface area of the box.
The manager of Sparklee Jewelry Store wants to calculate how much cardboard will be required to manufacture each box. If each box is created from a net, what will be the total amount of cardboard required, not counting any waste, to manufacture the box?
In the activity below, drag the dimensions to the appropriate place in the formula to calculate the total surface area of the box.
Now that you have correctly identified the dimensions, calculate the total surface area of the box.
Practice
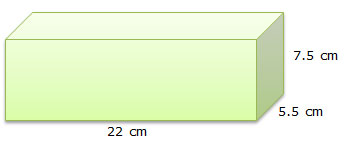
A pencil box is in the shape of a rectangular prism and has the dimensions shown below.
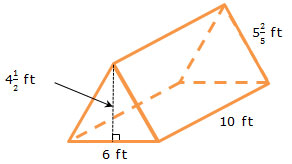
A tent is shaped like an isosceles triangular prism.
Determining Surface Areas of Cylinders
Cylinders will also frequently appear in surface area problems.
A sardine factory uses steel cans to package sardines. The cans are in the shape of cylinders. One can that they use is shown below.
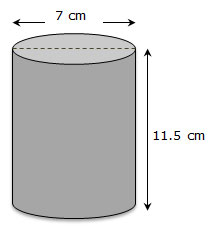
The factory engineer wants to know the area of the label of the can. Drag the dimensions to the appropriate place in the formula to calculate the lateral surface area of the can.
Now that you have correctly identified the dimensions, calculate the area of the label of the can, or the lateral surface area of the can.
The factory engineer also wants to know how much steel is required to manufacture one can. Drag the dimensions to the appropriate place in the formula to calculate the total surface area of the can.
Now that you have correctly identified the dimensions, calculate the amount of steel required to manufacture one can, or the total surface area of the can.
![]() View a video to see a detailed solution.
View a video to see a detailed solution.
Practice
1. A cylindrical poster tube is wrapped completely for shipping. What is the approximate amount of paper required, not counting any waste, to completely cover the cylinder?

2. A cylindrical water tank will be painted such that all exposed faces will be painted with weatherproof blue paint.

What will be the approximate total area of the water tank that is painted blue? Round your answer to the nearest hundredth.
Determining Surface Areas of Pyramids
A third 3-dimensional figure that you will encounter is a pyramid. Recall that a pyramid has only one polygon-shaped base, and the lateral faces are triangles instead of parallelograms or rectangles, like the lateral faces of a prism.
Pyramids are also named by the shape of their base. A triangular pyramid has a base in the shape of a triangle, a square pyramid has a base in the shape of a square, and a rectangular pyramid has a base in the shape of a rectangle.
The Westmoreland Junior High 8th Grade Spring Dance has the theme, A Night on the Nile. The school cafeteria will be decorated in an Egyptian theme. The centerpiece will be a large square pyramid.
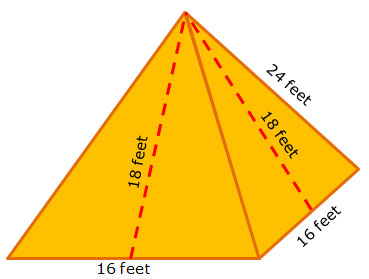
The class president wants to know the lateral surface area of the pyramid. Drag the dimensions to the appropriate place in the formula to calculate the lateral surface area of the pyramid.
Use the formula, S = Pl.
Now that you have correctly identified the dimensions, calculate the lateral surface area of the pyramid.
The 8th grade class vice president has decided that the entire pyramid should be a canvas tent, and the floor of the pyramid should also be lined with canvas. Drag the dimensions to the appropriate place in the formula to calculate the total surface area of the pyramid.
Use the formula, S = Pl + B.
Now that you have correctly identified the dimensions, calculate the total surface area of the pyramid.
Practice
1. A box in the shape of a square pyramid is used to wrap packages of candies.
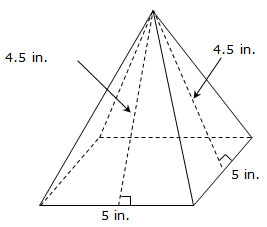
What is the total surface area of the box?
2. A decoration for a parade float will be in the shape of a rectangular pyramid. The people who designed the float have decided to paint the exposed faces of the pyramid. The pyramid will be resting on its base in the trailer used for the float.
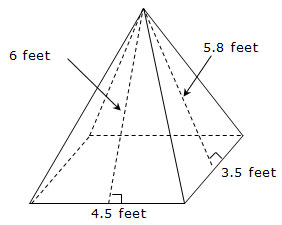
What will be the total area that is painted?
Summary
Finding the surface area of prisms, cylinders, and pyramids in application problems is a very important skill.
To summarize what you have learned in this lesson, watch the following videos showing additional examples of how to find the surface areas of these important 3-dimensional figures.
Source: brightstorm