Analyzing Similar Figures with Proportions
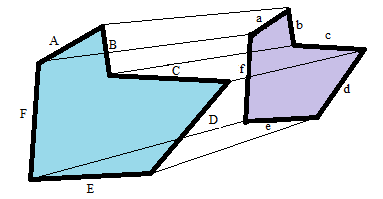
One common situation that can be represented with proportional relationships is analyzing similar figures. Similar figures are different sizes of the exact same shape.
When setting up a proportion for a pair of similar figures, you can only compare the lengths of corresponding sides. Corresponding sides are the matching sides of the similar figures. In the picture above, the corresponding sides are labeled with upper and lower case of the same letter.
Select the matching pairs by clicking on the tile that represents one of the corresponding sides or one of the equivalent ratios:
- Corresponding sides
- Equivalent ratios
One example of using similar figures is making scale drawings or models.
Read the following, and answer the questions below.

An architect is drawing a scale picture of a house. The dimensions of the actual rooms and the rooms in the picture are listed in the table below.
Copy the table into your notes, and fill in the missing information.
| Actual Measurement |
Process | Picture Measurement |
||
|---|---|---|---|---|
| Living Room |
Length |
20 Feet |
20 ( ) = 5 |
5 inches |
|
Width |
12 Feet |
12 ( ) = 3 |
3 inches |
|
| Dining Room |
Length |
18 Feet |
4.5 inches |
|
|
Width |
10 Feet |
|||
| Kitchen |
Length |
12 Feet |
||
|
Width |
16 Feet |
|||
| Bedroom |
Length |
12 Feet |
||
|
Width |
10 Feet |
|||
Click here to see the completed table.
- What do you notice is constant in the table?
- What proportional relationship could you use to relate p, a measurement in the picture, with a, an actual measurement?
- Given that y → picture measurement, k → and x → actual measurement use the variables ‘p’ and ‘a’ to rewrite the proportional relationship as an equation that looks like y = kx.
- If the architect were to measure one of the bathrooms in the house to be 10 feet long by 8 feet wide, what would the dimensions of the bathroom be in the picture?
- If the architect were to measure the length of a second bedroom in the house to be 15 feet long, what would the width of the second bedroom be in the picture?
Analyzing Similar Figures with Proportions—Example Problem
Anna is standing near a tree on a sunny day. She figures that she can calculate the height of the tree if she measures her shadow and the tree's shadow, and then uses a proportion.
Why can she use a proportion?
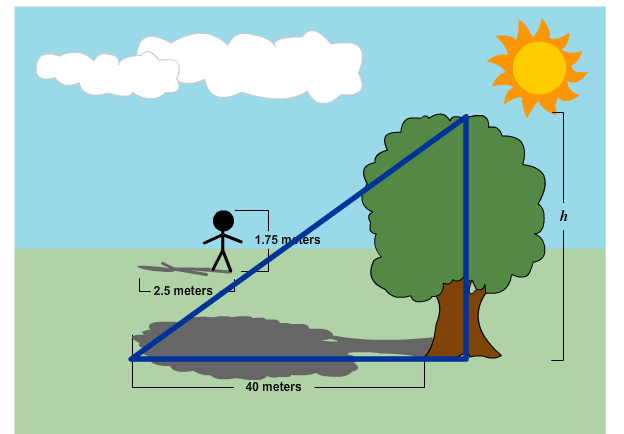
Copy the following table into your notes. Fill in the missing information.
|
Anna |
Tree |
|
|---|---|---|
|
Height |
||
|
Shadow |
Use the information in the table to write a proportional relationship that could be used to solve for h, the height of the tree.
Solve your proportion to determine the height of the tree. Two methods are shown below.
Proportions and Rates
Another common set of situations that can be represented by proportions are rate problems. Rates are ratios that compare two related quantities. The table below shows three examples of commonly used rates.
|
Rate |
Ratio |
Units |
|---|---|---|
|
Rate of Speed |
|
Miles per hour or meters per second |
|
Rate of Pay |
|
Dollars per week or per hour |
|
Prices |
|
Dollars per pound or per item |
What word do you notice in the units for each of these examples?
When a rate is given in a problem, the units often contain or are described by the word “per.”




|
Rate |
Ratio |
Units |
|---|---|---|
|
Margie can drive 95 miles in 1.5 hours. |
|
Miles per hour |
|
Steve built 15 birdhouses in 3 days. |
|
Birdhouses per day |
|
A 3-pound bag of onions cost $2.59. |
|
Dollars per pound |
|
Admission is $50 for 7 students. |
|
Price per student |
How can you use the units to help you set up the correct ratio for your proportion?
Read the example and answer the questions below.

Maria is reading a book for her English class. Last night, she read 84 pages in 2 hours. Tonight she plans to read for 5 hours. If she reads at the same rate tonight as she read last night, how many pages will she read tonight?
- What are the two related quantities that are being compared?
- What information is given in the problem that relates the two quantities?
- Does it make more sense to use this information in pages per hour or in hours per page?
- Write the information from the problem as a ratio.
- Use this ratio to set up a proportion that you could use to solve for p, the number of pages she reads in 5 hours.
- Solve your proportion for p.
 Tommy is helping his mom at the grocery store. He notices that potatoes are on sale, and you can buy a 5-pound bag for $2.29. Using the same unit rate, find the cost of a 7-pound bag of potatoes.
Tommy is helping his mom at the grocery store. He notices that potatoes are on sale, and you can buy a 5-pound bag for $2.29. Using the same unit rate, find the cost of a 7-pound bag of potatoes.
- What is the price rate written as a ratio?
- Write a proportion that could be used to calculate c, the cost of a 7-pound bag.
- Solve your proportion for c.