Let's Get Started
TEKS Standards and Student Expectations
A(3) Linear functions, equations, and inequalities. The student applies the mathematical process standards when using graphs of linear functions, key features, and related transformations to represent in multiple ways and solve, with and without technology, equations, inequalities, and systems of equations. The student is expected to:
A(3)(C) graph linear functions on the coordinate plane and identify key features, including x-intercept, y-intercept, zeros, and slope, in mathematical and real-world problems
Resource Objective(s)
Given algebraic, tabular, or graphical representations of linear functions, the student will determine the intercepts of the graphs and the zeros of the function.
Essential Questions
What is the relationship between the intercepts and the zeros of a function?
What method can be used to find the zero of a linear function?
What strategies can be used to solve for x- and y-intercepts?
Vocabulary
An Introduction to Intercepts and Zeros
Let's practice finding intercepts and zeros of linear functions. There are two types of intercepts: x-intercepts and y-intercepts. When you write an equation in slope-intercept form, the y-intercept is listed as b. The y-intercept is where the graph crosses the y-axis.
y = mx + b
The x-intercept is where the graph crosses the x-axis. What about the zeros of the linear function? The zero of the function is where the y-value is zero.
All three of these concepts can be seen by looking at a linear graph. Follow these directions to find the intercepts and the zero.
- Look for the y-intercept where the graph crosses the y-axis.
- Look for the x-intercept where the graph crosses the x-axis.
- Look for the zeros of the linear function where the y-value is zero.
Did you notice something unusual about steps 2 and 3? When you find where the x-intercept is located, the y-value is zero! That means that the zero of the linear function is the x-value of the x-intercept. So once you find #2, you can easily find #3.
Intercepts of Linear Functions from Graphs
Use this interactive applet to select a line, and find the y-intercept and the x-intercept of the graph.
Instructions:
- On the interactive graph, there are a red and blue dots.
- Put 0 in the equation for x, and solve for y. Move the red dot to the y-axis at that y value (the y-intercept).
When you have it correct, the word “Holla” will appear.
- Put 0 in the original equation for y, and solve x. Move the blue dot to the x-axis at that x value (the x-intercept).
When you are correct, the words “What? WHAT?!” and the line will appear.
- Select the circular arrows in the top right corner of the coordinate grid to get a new line.
After four or five, you can move on, but your are welcome to keep trying until you feel comfortable.
Intercepts of Linear Functions from Equations
Let's learn how to find the intercepts using an equation. To find the x-intercept, you solve the equation using y = 0. To find the y-intercept, you solve the equation using x = 0.
Use this interactive applet to practice changing equations to find the x-intercept and the y-intercept. At the top of the page, intercepts are explained. At the bottom of the page, there is an interactive activity for you to practice finding the intercepts of equations. Click on Linear Equations and Graphs after you have read the instructions.
Instructions:
- Read the information at the top of the page.
- Go to the applet at the bottom of the page.
- Click "Get New Example."
- Find the x-intercept and the y-intercept and type them into the boxes.
- Click "Check" to see if you are correct.
- If you are incorrect, it will tell you which one you have correct and will also give a hint.
Practice Finding Intercepts from Graphs
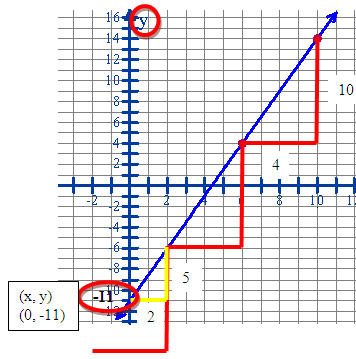
Practice finding intercepts in these problems. Some graphs (like the following one) actually show a line going through both intercepts, and you just need to be able to label them.
Exercise 1
Which coordinate points represent the x- and y-intercepts of the graph shown below?
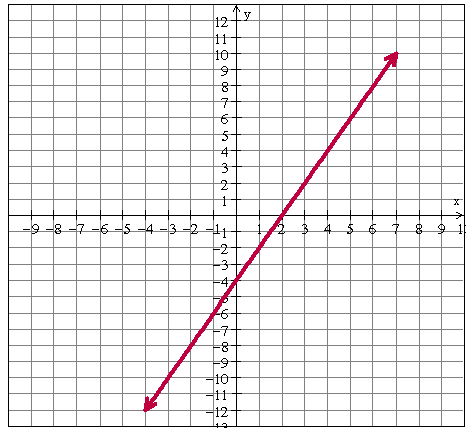
Hints
- Remind yourself that a coordinate is (x, y). An easy way to remember that is x comes before y in the alphabet.
- Circle the "x" and "y" labels on the axes if you have a problem remembering which is which.
- Label the points on the graph before selecting your answer.
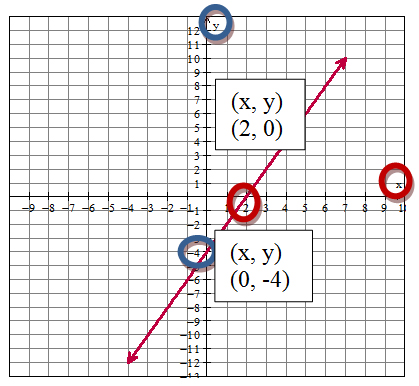
Practice Finding Intercepts
Some graphs actually show a line going through two points that are not the intercepts. You should re-graph those points on a piece of graph paper, and continue the lines through the intercepts.
Exercise 2
What is the y-intercept of the function graphed below?
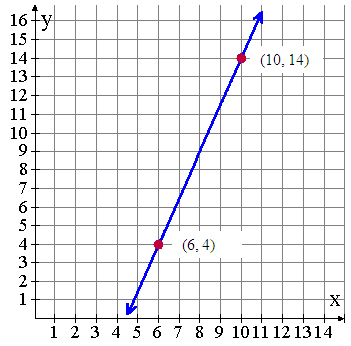
Hint
Re-graph the points given, and continue making points in the pattern of the slope.
Intercepts of Linear Functions from Tables
You can also find intercepts from a table by extending the pattern and checking the intercepts.
This table shows ordered pairs of a linear function. How could we find the intercepts?
| x | y |
| 9 | 2 |
| 3 | -2 |
| -3 | -6 |
| -9 | -10 |
Complete a table of common differences for x and y. To make a table of common differences, find the differences between the x-values. Then find the differences between the y-values.
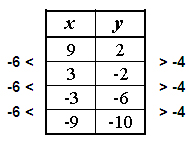
These common differences can be used to find the slope. The change in y divided by the change in x is the slope of a linear function. The slope is or . Plot the points, and continue across both intercepts to find the answers.

Zeros of Linear Functions
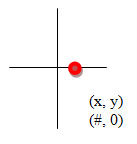
Finding the zero of a linear function is easy if you can find the x-intercept. The zero is the x-coordinate of the x-intercept.
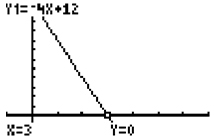
Let’s look at this example. What is the zero of the function ?
Hint (solving for x-intercept/zero):
Sketch and label an x-intercept so you can remember what it means.
Because you are solving for an x-intercept, plug in 0 for y and solve.
When given an equation, you can double check your answer on the graphing calculator by solving for y.
Solve for zero like this:
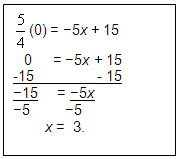
Check the solution on your graphing calculator like this:
Change the equation to slope-intercept form, and type it into the equation editor (Y=) as y = -4x + 12. In the graph screen, click TRACE to type in your answer and press enter. You can look also for the x-value with y = 0 in the table,.