Introduction
The relationship among the side lengths of right triangles was found to be of such high importance that several cultures took the time to study it and put it to use. Today, we call this relationship the Pythagorean Theorem.
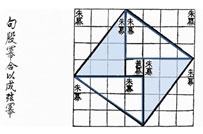
Most mathematicians believe that the Chinese were one of the first civilizations to observe the relationship known today as the Pythagorean Theorem.

It is also said that Mayans, Indians, and Egyptians used the Pythagorean Theorem to construct their buildings and pyramids.
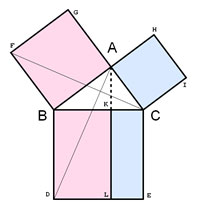
However, Greek mathematicians, including Pythagoras, were the first Western mathematicians to record the Pythagorean Theorem. Euclid, an ancient Greek mathematician, used triangles to prove the Pythagorean Theorem to be true.
In this lesson, you will examine different ways to represent the Pythagorean Theorem. As you do so, you will need to keep the following vocabulary terms in mind:
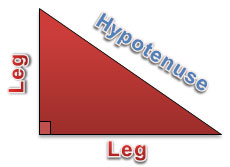
A right triangle has two legs, which are the sides adjacent to the right angle. The third side, which is opposite the right angle, is called the hypotenuse.
Sources of images used in this section as they appear, top to bottom:
- Chinese Pythagorean Theorem, Wikimedia Commons
- Manuel de Corselas, El Castillo o templo de Kukulkan. Chichén Itzá, México., Wikimedia Commons
- Jokes_Free4Me, Illustration_to_Euclid's_proof_of_the_Pythagorean_theorem, Wikimedia Commons
Modeling the Pythagorean Theorem Numerically
Let's begin by modeling the Pythagorean Theorem numerically.
In your notes, copy and paste the table below.
| Length of AC |
Length of BC |
Length of AB |
Area of Square AC |
Area of Square BC |
Area of Square AC + Area of BC |
Area of Square AB |
Use this link to fill in the table. Drag the sliders to adjust the lengths of the legs of triangle ABC. The interactive will calculate the lengths and areas for you.
- How does the length of AC compare to the area of Square AC?
- How does the length of BC compare to the area of Square BC?
- How does the length of AB compare to the area of Square AB?
- How does the area of Square AB compare to the sum of the areas of Square AC and Square BC?
- Write an algebraic equation to show the relationship between the length of AC, the length of BC, and the length of AB.
Modeling the Pythagorean Theorem Geometrically
The Pythagorean Theorem can also be shown geometrically. The interactive, A graphical proof of the Pythagorean Theorem, demonstrates how this works. Follow the steps by clicking the action buttons and following the six steps beneath the interactive.
How does the area of the largest square, alongside the hypotenuse, compare to the areas of the two smaller squares, alongside the legs?
Practice
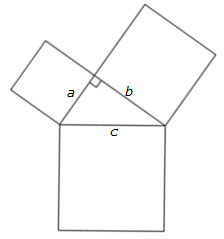
- If a = 3 and b = 4, what is the area of Square A and Square B?
- What will be the area of Square C?
- What will be the side length of Square C?
- What will be the perimeter of each square?
- If a = 5 and b = 12, what are the areas of all three squares?
- What will be the side length of Square C?
Consider the figure shown.
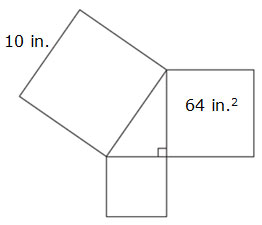
7. What is the area of the smallest square?
Using the Pythagorean Theorem
The Pythagorean Theorem can be written as follows:
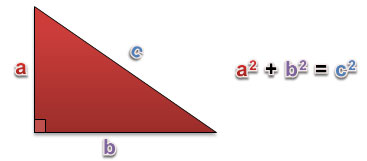
It is important to note that
- The Pythagorean Theorem can only be used for right triangles, and
- the Pythagorean Theorem can be used to determine any missing side length of a right triangle if you know the lengths of the two remaining sides.
You will investigate detailed real-world applications of the Pythagorean Theorem in a later lesson.
Examine the figures shown below. Sort them into two categories: those whose labeled sides demonstrate the Pythagorean Theorem and those whose labeled sides do not demonstrate the Pythagorean Theorem.
Practice
Identify which of the following triangles has side lengths a, b, and c that correctly demonstrate the Pythagorean Theorem.
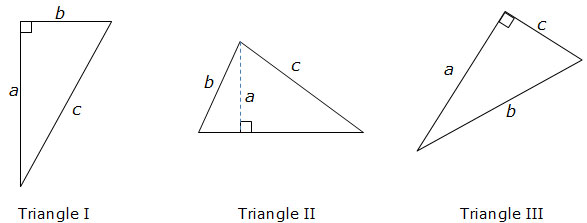
Summary
The Pythagorean Theorem is a highly useful formula in mathematics. The relationship between the three side lengths of a right triangle is so important, that many cultures discovered its use simultaneously.

The Egyptians used the Pythagorean Theorem to measure heights and distances.
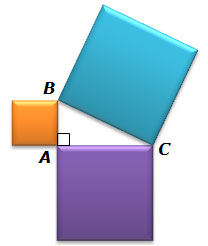
The Pythagorean Theorem uses squares to relate the side lengths of a right triangle. The sum of the areas of the squares whose sides make up the legs of the right triangle is equal to the area of the square whose side makes up the hypotenuse of the right triangle.
In other words,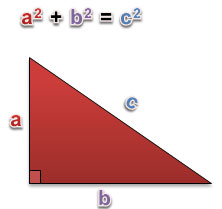
Sources of images used for this section as they appear, top to bottom:
Ikiwaner, All Gizah Pyramids, Wikimedia Commons