Introduction
Previously, you may have investigated translations, reflections, and dilations of two-dimensional figures on the coordinate plane. You also may have developed algebraic rules for each of these transformations.
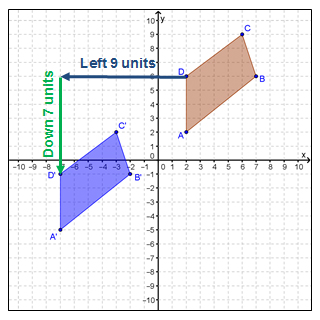
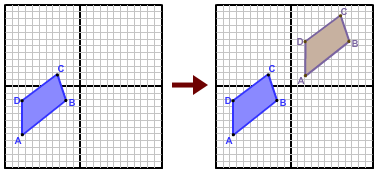
In the figure on the left, quadrilateral ABCD is translated left 9 units and down 7 units to create quadrilateral A'B'C'D'.
The algebraic rule for this translation is as follows:
(x, y) → (x − 9, y − 7)
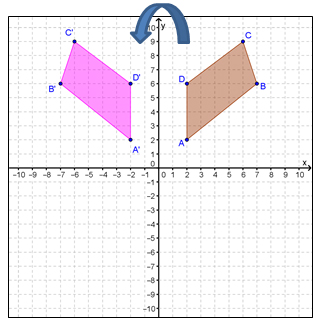
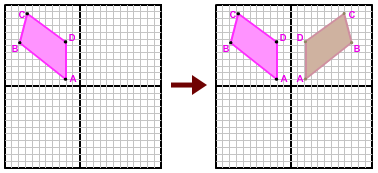
In the figure on the left, quadrilateral ABCD is reflected across the y-axis in order to generate quadrilateral A'B'C'D'.
The algebraic rule for this reflection is as follows:
(x, y) → (-x, y)
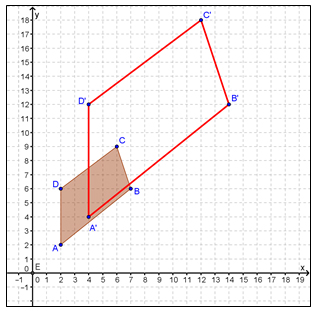
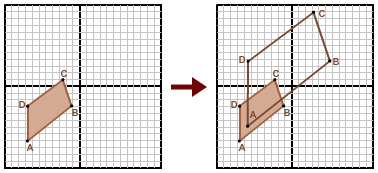
In the figure on the left, quadrilateral ABCD is dilated by a scale factor of 2 using the origin as the center of dilation in order to generate quadrilateral A'B'C'D'.
The algebraic rule for this reflection is as follows:
(x, y) → (2x, 2y)
In this lesson, you will first extend what you know about coordinate transformations to rotations of two-dimensional figures by 90°, 180°, and 270°. You will also distinguish between transformations that generate congruent figures and transformations that do not. Further, you will generalize particular attributes of figures, such as side lengths or angle measures that are preserved with different transformations.
Graphing Rotations on the Coordinate Plane
In the past, you investigated coordinate translations, reflections, and dilations. Translations are transformations that slide, or translate, a figure over a coordinate plane. Reflections are transformations that create mirror images of figures. Dilations are transformations that generate enlargements or reductions of figures.
In this section, you will extend what you know about coordinate transformations rotations in multiples of 90° and look for patterns in the coordinates.
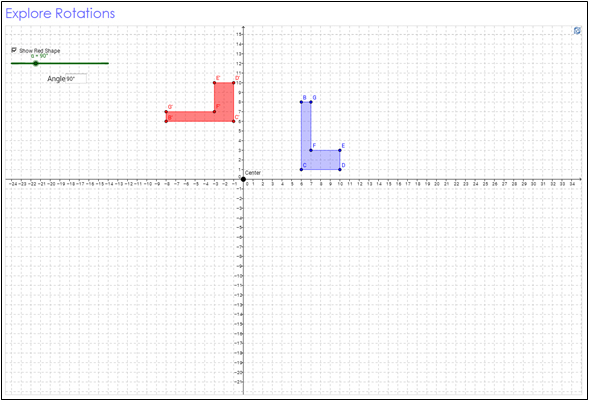
Part 1: 90° Rotations
Click the image below to open an interactive sketch in a new browser tab or window. Once you have opened the sketch, use the slider to change the angle of rotation to 90° counter-clockwise. Locate the coordinates of the image of the rotation, and complete the table below. Use your table to answer the questions that follow.
Click to see additional directions.
Use the interactive sketch to complete the following table for a 90° counter-clockwise rotation. Make a copy of the table in your notes. Fill in the columns for Original Coordinates using the coordinates of hexagon BCDEFG, which is the preimage of the rotation. Fill in the columns for Rotated Coordinates using the coordinates of hexagon B'C'D'E'F'G', which is the image of the rotation.
|
Image Point
|
Original
Coordinates |
Rotated
Coordinates |
|
B
|
||
|
C
|
||
|
D
|
||
|
E
|
||
|
F
|
||
|
G
|
Use your completed table to answer the questions that follow.
- What patterns do you observe in the coordinates?
- How could you express that relationship using an algebraic rule?
Part 2: 180° Rotations
Use the interactive sketch to complete the following table for a 180° counter-clockwise rotation. Make a copy of the table in your notes. Fill in the columns for Original Coordinates using the coordinates of hexagon BCDEFG, which is the preimage of the rotation. Fill in the columns for Rotated Coordinates using the coordinates of hexagon B'C'D'E'F'G', which is the image of the rotation.
|
Image Point
|
Original
Coordinates |
Rotated
Coordinates |
|
B
|
||
|
C
|
||
|
D
|
||
|
E
|
||
|
F
|
||
|
G
|
Use your completed table to answer the questions that follow.
- What patterns do you observe in the coordinates?
- How could you express that relationship using an algebraic rule?
Part 3: 270° Rotations
Use the interactive sketch to complete the following table for a 270° counter-clockwise rotation. Make a copy of the table in your notes. Fill in the columns for Original Coordinates using the coordinates of hexagon BCDEFG, which is the preimage of the rotation. Fill in the columns for Rotated Coordinates using the coordinates of hexagon B'C'D'E'F'G', which is the image of the rotation.
|
Image Point
|
Original
Coordinates |
Rotated
Coordinates |
|
B
|
||
|
C
|
||
|
D
|
||
|
E
|
||
|
F
|
||
|
G
|
Use your completed table to answer the questions that follow.
- What patterns do you observe in the coordinates?
- How could you express that relationship using an algebraic rule?
Part 4: 360° Rotations
Use the interactive sketch to change the angle of rotation to 360° counter-clockwise. Use the results to answer the questions that follow.
- What happens to the image of the rotation when the preimage is rotated 360°? Why do you think that is the case?
- How could you express that relationship using an algebraic rule?
Pause and Reflect
How are a 90° counterclockwise rotation about the origin and a 270° clockwise rotation alike? How are they different?
Practice
1. The figure below shows quadrilateral WXYZ.
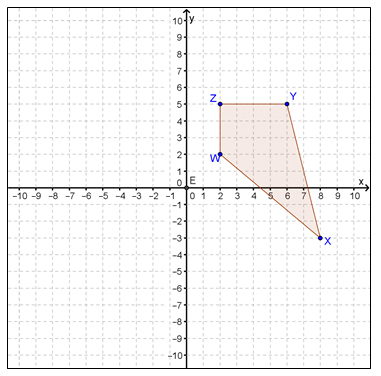
If WXYZ is rotated 90° counterclockwise about the origin, what will be the coordinates of the image of WXYZ?
2. In the figure below, pentagon PQRST has been rotated counterclockwise about the origin to generate pentagon P'Q'R'S'T'.
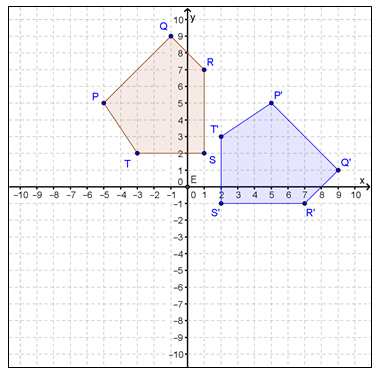
What is the algebraic rule that best describes the rotation?
3. Which of the following pairs of transformations would generate the same image from the same preimage?
I. Rotation of 270° counterclockwise about the origin and rotation of 90° clockwise about the origin.
II. Rotation of 180° about the origin and reflection across the line y = -x
III. Rotation of 90° clockwise about the origin and translation of 4 units right and 5 units down
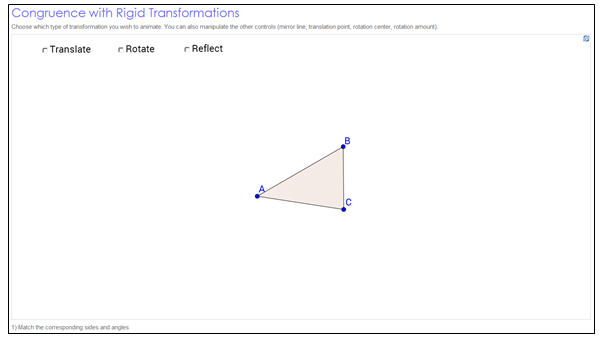
Comparing Side Lengths and Angle Measures in Transformations

In the last section, you added rotations to your set of transformations, along with reflections, translations, and dilations. In this section, you will compare two different classes of transformations: (1) congruence transformations that generate an image that is congruent to the preimage and (2) non-congruence transformations that generate an image that is not congruent to the preimage. Specifically, you will use side lengths and angle measures to distinguish between which types of transformations are congruence transformations, and which types are not.
- Select the translate option.
- Use the slider to translate Δ ABC, and use the check boxes to reveal the side lengths and angle measures for both Δ ABC and its translated image.
- Move the red Translate Point to adjust the translation.
- Use the interactive to answer the following questions.
Need additional directions for translations?
- What do you notice about the lengths of corresponding sides for both the preimage (Δ ABC) and the translated image (Δ A'''B'''C''')?
- What do you notice about the measures of corresponding angles for both the preimage (Δ ABC) and the translated image (Δ A'''B'''C''')?
- Is Δ ABC, the preimage, congruent to Δ A'''B'''C''', the image? How do you know?
Rotations
- Click the double arrow in the top right corner of the sketch to reset the sketch.
- Select the Rotate option.
- Enter the desired angle of rotation.
- Use the slider to rotate Δ ABC, and use the check boxes to reveal the side lengths and angle measures for both Δ ABC and its rotated image.
- Move the red Rotation Center point to adjust the center of rotation.
- Repeat the process for several different angles of rotation.
- Use the interactive to answer the following questions.
Need additional directions for rotations?
- What do you notice about the lengths of corresponding sides for both the preimage (Δ ABC) and the rotated image (Δ A'B'C')?
- What do you notice about the measures of corresponding angles for both the preimage (Δ ABC) and the rotated image (Δ A'B'C')?
- Is Δ ABC, the preimage, congruent to Δ A'B'C', the image? How do you know?
Reflections
- Click the double arrow in the top right corner of the sketch to reset the sketch.
- Select the Reflect option.
- Use the slider to reflect Δ ABC fully, and use the check boxes to reveal the side lengths and angle measures for both Δ ABC and its rotated image.
- Move the red Mirror Line points to adjust the line of reflection.
- Use the interactive to answer the following questions.
Need additional directions for reflections?
- What do you notice about the lengths of corresponding sides for both the preimage (Δ ABC) and the reflected image (Δ A''B''C'')?
- What do you notice about the measures of corresponding angles for both the preimage (Δ ABC) and the reflected image (Δ A''B''C'')?
- Is Δ ABC, the preimage, congruent to Δ A''B''C'', the image? How do you know?
Dilations
Use the interactive below to investigate side lengths and angle relationships for dilations. Use the slider to adjust the scale factor of the dilation, and drag point D to adjust the center of dilation. Use the interactive to answer the questions that follow.
Properties of Dilations
OnTRACK for College Readiness, Created with GeoGebra |
Need additional directions for dilations?
- What do you notice about the lengths of corresponding sides for both the preimage (Δ ABC) and the dilated image (Δ A'B'C')?
- What do you notice about the measures of corresponding angles for both the preimage (Δ ABC) and the reflected image (Δ A'B'C')?
- Is Δ ABC, the preimage, congruent to Δ A'B'C', the image? How do you know?
Pause and Reflect
- A congruence transformation is a transformation in which the preimage and image are congruent figures. Which transformation(s) are congruence transformations?
- A non-congruence transformation is a transformation in which the preimage and image are not congruent figures. Which transformation(s) are non-congruence transformations?
- Which transformations preserve angle measures between the preimage and the image?
- Which transformations preserve side lengths between the preimage and the image?
Practice
1. Which of the following properties about geometric transformations are true?
I. Dilations preserve congruence while reflections do not.
II. Rotations and reflections both preserve a polygon’s side lengths.
III. Dilations and translations both preserve a polygon’s angle measures.
2. Trapezoid ABCD is transformed using the transformation (x, y) → (x − 4, y + 5). Which of the following statements about ABCD and A'B'C'D' are true?
I. ABCD is congruent to A'B'C'D'.
II. The corresponding angles of the two trapezoids are congruent, but the corresponding sides of the two trapezoids are not.
III. A'B'C'D' is a translation of ABCD.
3. Which of the following transformations are congruence transformations?
I. (x, y) → (−y, x)
II. (x, y) → (x, −y)
III. (x, y) → (1.5x, 1.5y)
Summary
In this lesson, you extended what you knew about translations, reflections, and dilations to include rotations. You also distinguished between congruence transformations (translations, reflections, and rotations) and non-congruence transformations (dilations).