Learning Objectives
Learning Objectives
By the end of this section, you will be able to do the following:
- Explain Kepler’s three laws of planetary motion
- Apply Kepler’s laws to calculate characteristics of orbits
| aphelion | Copernican model | eccentricity |
| Kepler’s laws of planetary motion | perihelion | Ptolemaic model |
Concepts Related to Kepler’s Laws of Planetary Motion
Concepts Related to Kepler’s Laws of Planetary Motion
Examples of orbits abound. Hundreds of artificial satellites orbit Earth together with thousands of pieces of debris. The moon’s orbit around Earth has intrigued humans from time immemorial. The orbits of planets, asteroids, meteors, and comets around the sun are no less interesting. If we look farther, we see almost unimaginable numbers of stars, galaxies, and other celestial objects orbiting one another and interacting through gravity.
All these motions are governed by gravitational force. The orbital motions of objects in our own solar system are simple enough to describe with a few fairly simple laws. The orbits of planets and moons satisfy the following two conditions:
- The mass of the orbiting object, m, is small compared to the mass of the object it orbits, M.
- The system is isolated from other massive objects.
Based on the motion of the planets about the sun, Kepler devised a set of three classical laws, called Kepler’s laws of planetary motion, that describe the orbits of all bodies satisfying these two conditions:
- The orbit of each planet around the sun is an ellipse with the sun at one focus.
- Each planet moves so that an imaginary line drawn from the sun to the planet sweeps out equal areas in equal times.
- The ratio of the squares of the periods of any two planets about the sun is equal to the ratio of the cubes of their average distances from the sun.
These descriptive laws are named for the German astronomer Johannes Kepler (1571–1630). He devised them after careful study (over some 20 years) of a large amount of meticulously recorded observations of planetary motion done by Tycho Brahe (1546–1601). Such careful collection and detailed recording of methods and data are hallmarks of good science. Data constitute the evidence from which new interpretations and meanings can be constructed. Let’s look closer at each of these laws.
Kepler’s First Law
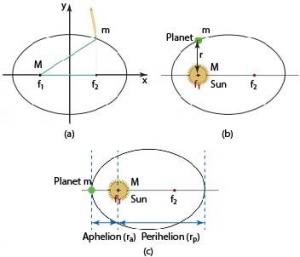
The orbit of each planet about the sun is an ellipse with the sun at one focus, as shown in Figure 7.2. The planet’s closest approach to the sun is called perihelion and its farthest distance from the sun is called aphelion.
If you know the aphelion (ra) and perihelion (rp) distances, then you can calculate the semi-major axis (a) and semi-minor axis (b).
Kepler’s Second Law
Each planet moves so that an imaginary line drawn from the sun to the planet sweeps out equal areas in equal times, as shown in Figure 7.4.
Tips For Success
Note that while, for historical reasons, Kepler’s laws are stated for planets orbiting the sun, they are actually valid for all bodies satisfying the two previously stated conditions.
Kepler’s Third Law
The ratio of the periods squared of any two planets around the sun is equal to the ratio of their average distances from the sun cubed. In equation form, this is
where T is the period (time for one orbit) and r is the average distance (also called orbital radius). This equation is valid only for comparing two small masses orbiting a single large mass. Most importantly, this is only a descriptive equation; it gives no information about the cause of the equality.
Links To Physics
History: Ptolemy vs. Copernicus
Before the discoveries of Kepler, Copernicus, Galileo, Newton, and others, the solar system was thought to revolve around Earth as shown in Figure 7.5 (a). This is called the Ptolemaic model, named for the Greek philosopher Ptolemy who lived in the second century AD. The Ptolemaic model is characterized by a list of facts for the motions of planets, with no explanation of cause and effect. There tended to be a different rule for each heavenly body and a general lack of simplicity.
Figure 7.5 (b) represents the modern or Copernican model. In this model, a small set of rules and a single underlying force explain not only all planetary motion in the solar system, but also all other situations involving gravity. The breadth and simplicity of the laws of physics are compelling.
Nicolaus Copernicus (1473–1543) first had the idea that the planets circle the sun, in about 1514. It took him almost 20 years to work out the mathematical details for his model. He waited another 10 years or so to publish his work. It is thought he hesitated because he was afraid people would make fun of his theory. Actually, the reaction of many people was more one of fear and anger. Many people felt the Copernican model threatened their basic belief system. About 100 years later, the astronomer Galileo was put under house arrest for providing evidence that planets, including Earth, orbited the sun. In all, it took almost 300 years for everyone to admit that Copernicus had been right all along.
Explain why Earth does actually appear to be the center of the solar system.
- Earth appears to be the center of the solar system because Earth is at the center of the universe, and everything revolves around it in a circular orbit.
- Earth appears to be the center of the solar system because, in the reference frame of Earth, the sun, moon, and planets all appear to move across the sky as if they were circling Earth.
- Earth appears to be at the center of the solar system because Earth is at the center of the solar system and all the heavenly bodies revolve around it.
- Earth appears to be at the center of the solar system because Earth is located at one of the foci of the elliptical orbit of the sun, moon, and other planets.
Virtual Physics
Acceleration
This simulation allows you to create your own solar system so that you can see how changing distances and masses determines the orbits of planets. Click Help for instructions.
- The orbiting object moves fastest when it is closest to the central object and slowest when it is farthest away.
- The orbiting object moves slowest when it is closest to the central object and fastest when it is farthest away.
- The orbiting object moves with the same speed at every point on the circumference of the elliptical orbit.
- There is no relationship between the speed of the object and the location of the planet on the circumference of the orbit.
Calculations Related to Kepler’s Laws of Planetary Motion
Calculations Related to Kepler’s Laws of Planetary Motion
Kepler’s First Law
Refer back to this figure (a). Notice which distances are constant. The foci are fixed, so distance is a constant. The definition of an ellipse states that the sum of the distances is also constant. These two facts taken together mean that the perimeter of triangle must also be constant. Knowledge of these constants will help you determine positions and distances of objects in a system that includes one object orbiting another.
Kepler’s Second Law
Refer back to this figure. The second law says that the segments have equal area and that it takes equal time to sweep through each segment. That is, the time it takes to travel from A to B equals the time it takes to travel from C to D, and so forth. Velocity v equals distance d divided by time t: . Then, , so distance divided by velocity is also a constant. For example, if we know the average velocity of Earth on June 21 and December 21, we can compare the distance Earth travels on those days.
The degree of elongation of an elliptical orbit is called its eccentricity (e). Eccentricity is calculated by dividing the distance f from the center of an ellipse to one of the foci by half the long axis a.
When , the ellipse is a circle.
The area of an ellipse is given by , where b is half the short axis. If you know the axes of Earth’s orbit and the area Earth sweeps out in a given period of time, you can calculate the fraction of the year that has elapsed.
Worked Example
Kepler’s First Law
At its closest approach, a moon comes within 200,000 km of the planet it orbits. At that point, the moon is 300,000 km from the other focus of its orbit, f2. The planet is focus f1 of the moon’s elliptical orbit. How far is the moon from the planet when it is 260,000 km from f2?
Strategy
Show and label the ellipse that is the orbit in your solution. Picture the triangle f1mf2 collapsed along the major axis and add up the lengths of the three sides. Find the length of the unknown side of the triangle when the moon is 260,000 km from f2.
Perimeter of
The perimeter of triangle f1mf2 must be constant because the distance between the foci does not change and Kepler’s first law says the orbit is an ellipse. For any ellipse, the sum of the two sides of the triangle, which are f1m and mf2, is constant.
Worked Example
Kepler’s Second Law
Figure 7.7 shows the major and minor axes of an ellipse. The semi-major and semi-minor axes are half of these, respectively.
Earth’s orbit is slightly elliptical, with a semi-major axis of 152 million km and a semi-minor axis of 147 million km. If Earth’s period is 365.26 days, what area does an Earth-to-sun line sweep past in one day?
Strategy
Each day, Earth sweeps past an equal-sized area, so we divide the total area by the number of days in a year to find the area swept past in one day. For total area use . Calculate A, the area inside Earth’s orbit and divide by the number of days in a year (i.e., its period).
The area swept out in one day is thus .
The answer is based on Kepler’s law, which states that a line from a planet to the sun sweeps out equal areas in equal times.
Kepler’s Third Law
Kepler’s third law states that the ratio of the squares of the periods of any two planets (T1, T2) is equal to the ratio of the cubes of their average orbital distance from the sun (r1, r2). Mathematically, this is represented by
From this equation, it follows that the ratio r3/T2 is the same for all planets in the solar system. Later we will see how the work of Newton leads to a value for this constant.
Worked Example
Kepler’s Third Law
Given that the moon orbits Earth each 27.3 days and that it is an average distance of from the center of Earth, calculate the period of an artificial satellite orbiting at an average altitude of 1,500 km above Earth’s surface.
Strategy
The period, or time for one orbit, is related to the radius of the orbit by Kepler’s third law, given in mathematical form by . Let us use the subscript 1 for the moon and the subscript 2 for the satellite. We are asked to find T2. The given information tells us that the orbital radius of the moon is , and that the period of the moon is . The height of the artificial satellite above Earth’s surface is given, so to get the distance r2 from the center of Earth we must add the height to the radius of Earth (6380 km). This gives . Now all quantities are known, so T2 can be found.
To solve for T2, we cross-multiply and take the square root, yielding
This is a reasonable period for a satellite in a fairly low orbit. It is interesting that any satellite at this altitude will complete one orbit in the same amount of time.
Practice Problems
Practice Problems
A planet with no axial tilt is located in another solar system. It circles its sun in a very elliptical orbit so that the temperature varies greatly throughout the year. If the year there has 612 days and the inhabitants celebrate the coldest day on day 1 of their calendar, when is the warmest day?
- Day 1
- Day 153
- Day 306
- Day 459
Check Your Understanding
Check Your Understanding
- Kepler’s laws are purely descriptive.
- Kepler’s laws are purely causal.
- Kepler’s laws are descriptive as well as causal.
- Kepler’s laws are neither descriptive nor causal.
True or false—According to Kepler’s laws of planetary motion, a satellite increases its speed as it approaches its parent body and decreases its speed as it moves away from the parent body.
- True
- False
- One focus is the parent body, and the other is located at the opposite end of the ellipse, at the same distance from the center as the parent body.
- One focus is the parent body, and the other is located at the opposite end of the ellipse, at half the distance from the center as the parent body.
- One focus is the parent body and the other is located outside of the elliptical orbit, on the line on which is the semi-major axis of the ellipse.
- One focus is on the line containing the semi-major axis of the ellipse, and the other is located anywhere on the elliptical orbit of the satellite.