Learning Objectives
Learning Objectives
By the end of this section, you will be able to do the following:
- Define components of vectors
- Describe the analytical method of vector addition and subtraction
- Use the analytical method of vector addition and subtraction to solve problems
| analytical method | component (of a two-dimensional vector) |
Components of Vectors
Components of Vectors
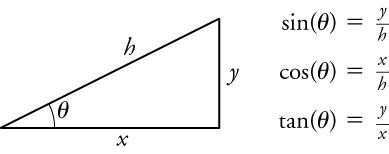
For the analytical method of vector addition and subtraction, we use some simple geometry and trigonometry, instead of using a ruler and protractor as we did for graphical methods. However, the graphical method will still come in handy to visualize the problem by drawing vectors using the head-to-tail method. The analytical method is more accurate than the graphical method, which is limited by the precision of the drawing. For a refresher on the definitions of the sine, cosine, and tangent of an angle, see Figure 5.18.
Since, by definition, , we can find the length x if we know h and by using . Similarly, we can find the length of y by using . These trigonometric relationships are useful for adding vectors.
When a vector acts in more than one dimension, it is useful to break it down into its x and y components. For a two-dimensional vector, a component is a piece of a vector that points in either the x- or y-direction. Every 2-d vector can be expressed as a sum of its x and y components.
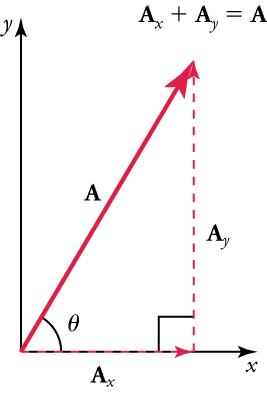
For example, given a vector likein Figure 5.19, we may want to find what two perpendicular vectors,and, add to produce it. In this example,andform a right triangle, meaning that the angle between them is 90 degrees. This is a common situation in physics and happens to be the least complicated situation trigonometrically.
andare defined to be the components ofalong the x- and y-axes. The three vectors,,, and, form a right triangle.
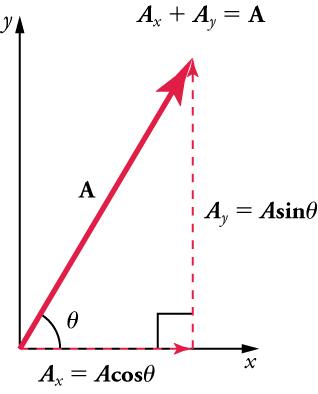
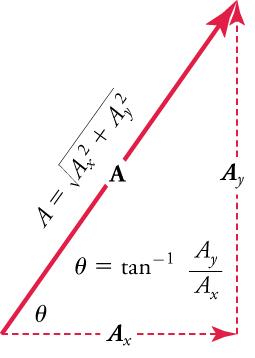
If the vectoris known, then its magnitude(its length) and its angle(its direction) are known. To findand, its x- and y-components, we use the following relationships for a right triangle:
and
whereis the magnitude of A in the x-direction,is the magnitude of A in the y-direction, andis the angle of the resultant with respect to the x-axis, as shown in Figure 5.20.
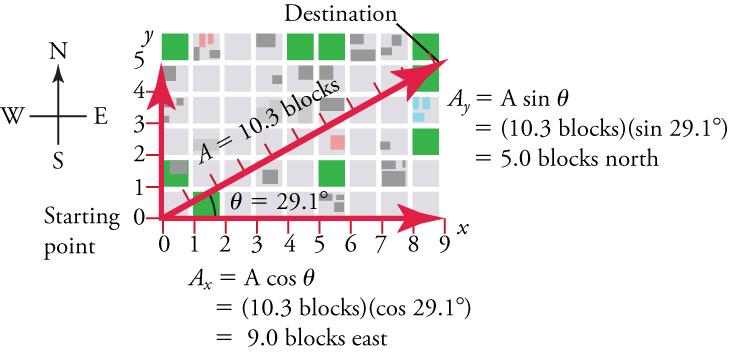
Suppose, for example, thatis the vector representing the total displacement of the person walking in a city, as illustrated in Figure 5.21.
Then A = 10.3 blocks and , so that
This magnitude indicates that the walker has traveled 9 blocks to the east—in other words, a 9-block eastward displacement. Similarly,
indicating that the walker has traveled 5 blocks to the north—a 5-block northward displacement.
Analytical Method of Vector Addition and Subtraction
Analytical Method of Vector Addition and Subtraction
Calculating a resultant vector (or vector addition) is the reverse of breaking the resultant down into its components. If the perpendicular components and of a vector are known, then we can find analytically. How do we do this? Since, by definition,
we solve for to find the direction of the resultant.
Since this is a right triangle, the Pythagorean theorem (x2 + y2 = h2) for finding the hypotenuse applies. In this case, it becomes
Solving for A gives
In summary, to find the magnitude and direction of a vector from its perpendicular components and , as illustrated in Figure 5.22, we use the following relationships:
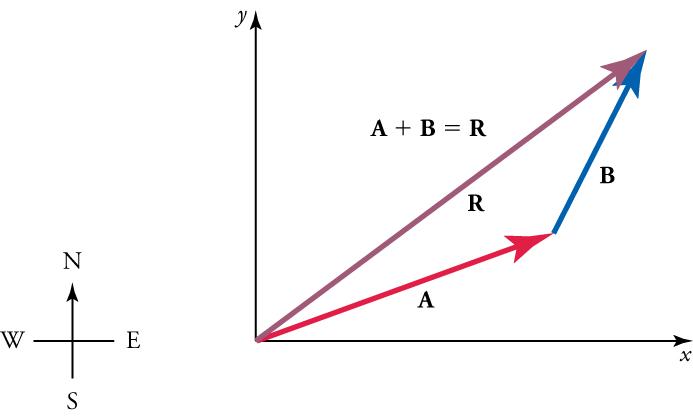
Sometimes, the vectors added are not perfectly perpendicular to one another. An example of this is the case below, where the vectors and are added to produce the resultant as illustrated in Figure 5.23.
Ifandrepresent two legs of a walk (two displacements), thenis the total displacement. The person taking the walk ends up at the tip of. There are many ways to arrive at the same point. The person could have walked straight ahead first in the x-direction and then in the y-direction. Those paths are the x- and y-components of the resultant,andIf we knowand, we can findandusing the equationsand.
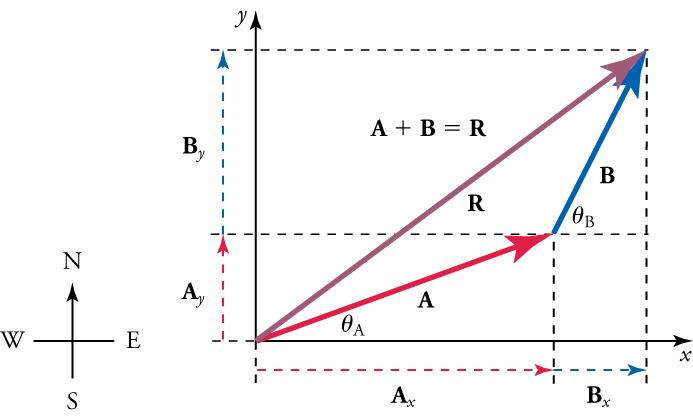
- Draw in the x and y components of each vector (including the resultant) with a dashed line. Use the equationsandto find the components. In Figure 5.24, these components are,,, andVectormakes an angle ofwith the x-axis, and vectormakes and angle ofwith its own x-axis (which is slightly above the x-axis used by vector A).
Figure 5.24 To add vectorsandfirst determine the horizontal and vertical components of each vector. These are the dotted vectorsshown in the image.
- Find the x component of the resultant by adding the x component of the vectors
and find the y component of the resultant (as illustrated in Figure 5.25) by adding the y component of the vectors.
Figure 5.25 The vectorsandadd to give the magnitude of the resultant vector in the horizontal direction,Similarly, the vectorsandadd to give the magnitude of the resultant vector in the vertical direction,Now that we know the components of we can find its magnitude and direction.
- To get the magnitude of the resultant R, use the Pythagorean theorem.
- To get the direction of the resultant
Watch Physics
Classifying Vectors and Quantities Example
This video contrasts and compares three vectors in terms of their magnitudes, positions, and directions.
- . All of them will cancel each other out.
- . Two of them will cancel each other out.
- . Two of them will add together to give the resultant.
- units. All of them will add together to give the resultant.
Tips For Success
In the video, the vectors were represented with an arrow above them rather than in bold. This is a common notation in math classes.
Using the Analytical Method of Vector Addition and Subtraction to Solve Problems
Using the Analytical Method of Vector Addition and Subtraction to Solve Problems
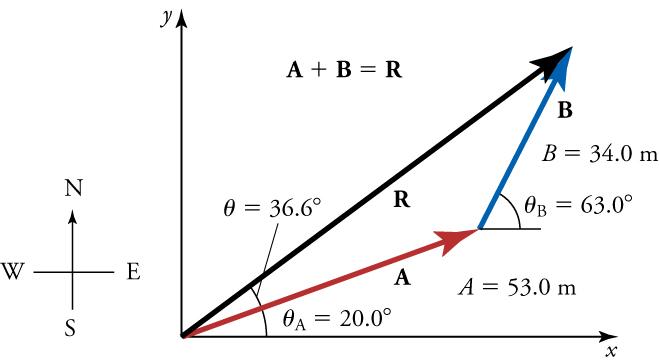
Figure 5.26 uses the analytical method to add vectors.
Worked Example
Add the vectorto the vectorshown in Figure 5.26, using the steps above. The x-axis is along the east–west direction, and the y-axis is along the north–south directions. A person first walksin a directionnorth of east, represented by vectorThe person then walksin a directionnorth of east, represented by vector
Strategy
The components ofandalong the x- and y-axes represent walking due east and due north to get to the same ending point. We will solve for these components and then add them in the x-direction and y-direction to find the resultant.
First, we find the components ofandalong the x- and y-axes. From the problem, we know that,,=, and. We find the x-components by using, which gives
and
Similarly, the y-components are found using
and
The x- and y-components of the resultant are
and
Now we can find the magnitude of the resultant by using the Pythagorean theorem
so that
Finally, we find the direction of the resultant
This is
This example shows vector addition using the analytical method. Vector subtraction using the analytical method is very similar. It is just the addition of a negative vector. That is,. The components of –are the negatives of the components of. Therefore, the x- and y-components of the resultant are
and
and the rest of the method outlined above is identical to that for addition.
Practice Problems
What is the magnitude of a vector whose x-component is 4 cm and whose y-component is 3 cm?
- 1 cm
- 5 cm
- 7 cm
- 25 cm
What is the magnitude of a vector that makes an angle of 30° to the horizontal and whose x-component is 3 units?
- 2.61 units
- 3.00 units
- 3.46 units
- 6.00 units
Links To Physics
Atmospheric Science
Atmospheric science is a physical science, meaning that it is a science based heavily on physics. Atmospheric science includes meteorology (the study of weather) and climatology (the study of climate). Climate is basically the average weather over a longer time scale. Weather changes quickly over time, whereas the climate changes more gradually.
The movement of air, water and heat is vitally important to climatology and meteorology. Since motion is such a major factor in weather and climate, this field uses vectors for much of its math.
Vectors are used to represent currents in the ocean, wind velocity and forces acting on a parcel of air. You have probably seen a weather map using vectors to show the strength (magnitude) and direction of the wind.
Vectors used in atmospheric science are often three-dimensional. We won’t cover three-dimensional motion in this text, but to go from two-dimensions to three-dimensions, you simply add a third vector component. Three-dimensional motion is represented as a combination of x-, y- and z components, where z is the altitude.
Vector calculus combines vector math with calculus, and is often used to find the rates of change in temperature, pressure or wind speed over time or distance. This is useful information, since atmospheric motion is driven by changes in pressure or temperature. The greater the variation in pressure over a given distance, the stronger the wind to try to correct that imbalance. Cold air tends to be more dense and therefore has higher pressure than warm air. Higher pressure air rushes into a region of lower pressure and gets deflected by the spinning of the Earth, and friction slows the wind at Earth’s surface.
Finding how wind changes over distance and multiplying vectors lets meteorologists, like the one shown in Figure 5.27, figure out how much rotation (spin) there is in the atmosphere at any given time and location. This is an important tool for tornado prediction. Conditions with greater rotation are more likely to produce tornadoes.
- Vectors have magnitude as well as direction and can be quickly solved through scalar algebraic operations.
- Vectors have magnitude but no direction, so it becomes easy to express physical quantities involved in the atmospheric science.
- Vectors can be solved very accurately through geometry, which helps to make better predictions in atmospheric science.
- Vectors have magnitude as well as direction and are used in equations that describe the three dimensional motion of the atmosphere.
Check Your Understanding
Check Your Understanding
Between the analytical and graphical methods of vector additions, which is more accurate? Why?
- The analytical method is less accurate than the graphical method, because the former involves geometry and trigonometry.
- The analytical method is more accurate than the graphical method, because the latter involves some extensive calculations.
- The analytical method is less accurate than the graphical method, because the former includes drawing all figures to the right scale.
- The analytical method is more accurate than the graphical method, because the latter is limited by the precision of the drawing.
What is a component of a two dimensional vector?
- A component is a piece of a vector that points in either the x or y direction.
- A component is a piece of a vector that has half of the magnitude of the original vector.
- A component is a piece of a vector that points in the direction opposite to the original vector.
- A component is a piece of a vector that points in the same direction as original vector but with double of its magnitude.
How can we determine the magnitude of a vector if we know the magnitudes of its components?