Learning Objectives
Learning Objectives
By the end of the section, you will be able to do the following:
- Define, describe, and differentiate the four fundamental forces
- Describe the carrier particles and explain how their exchange transmits force
- Explain how particle accelerators work to gather evidence about particle physics
| carrier particle | colliding beam | cyclotron |
| Feynman diagram | graviton | particle physics |
| pion | quantum electrodynamics | synchrotron |
| boson | boson | weak nuclear force |
| boson |
Despite the apparent complexity within the universe, there remain just four basic forces. These forces are responsible for all interactions known to science: from the very small to the very large to those that we experience in our day-to-day lives. These forces describe the movement of galaxies, the chemical reactions in our laboratories, the structure within atomic nuclei, and the cause of radioactive decay. They describe the true cause behind familiar terms like friction and the normal force. These four basic forces are known as fundamental because they alone are responsible for all observations of forces in nature. The four fundamental forces are gravity, electromagnetism, weak nuclear force, and strong nuclear force.
Understanding the Four Forces
Understanding the Four Forces
The gravitational force is most familiar to us because it describes so many of our common observations. It explains why a dropped ball falls to the ground and why our planet orbits the Sun. It gives us the property of weight and determines much about the motion of objects in our daily lives. Because gravitational force acts between all objects of mass and has the ability to act over large distances, the gravitational force can be used to explain much of what we observe and can even describe the motion of objects on astronomical scales! That said, gravity is incredibly weak compared to the other fundamental forces and is the weakest of all of the fundamental forces. Consider this: The entire mass of Earth is needed to hold an iron nail to the ground. Yet with a simple magnet, the force of gravity can be overcome, allowing the nail to accelerate upward through space.
The electromagnetic force is responsible for both electrostatic interactions and the magnetic force seen between bar magnets. When focusing on the electrostatic relationship between two charged particles, the electromagnetic force is known as the coulomb force. The electromagnetic force is an important force in the chemical and biological sciences, as it is responsible for molecular connections like ionic bonding and hydrogen bonding. Additionally, the electromagnetic force is behind the common physics forces of friction and the normal force. Like the gravitational force, the electromagnetic force is an inverse square law. However, the electromagnetic force does not exist between any two objects of mass, only those that are charged.
When considering the structure of an atom, the electromagnetic force is somewhat apparent. After all, the electrons are held in place by an attractive force from the nucleus. But what causes the nucleus to remain intact? After all, if all protons are positive, it makes sense that the coulomb force between the protons would repel the nucleus apart immediately. Scientists theorized that another force must exist within the nucleus to keep it together. They further theorized that this nuclear force must be significantly stronger than gravity, which has been observed and measured for centuries, and also stronger than the electromagnetic force, which would cause the protons to want to accelerate away from each other.
The strong nuclear force is an attractive force that exists between all nucleons. This force, which acts equally between proton-proton connections, proton-neutron connections, and neutron-neutron connections, is the strongest of all forces at short ranges. However, at a distance of 10–13 cm, or the diameter of a single proton, the force dissipates to zero. If the nucleus is large (it has many nucleons), then the distance between each nucleon could be much larger than the diameter of a single proton.
The weak nuclear force is responsible for beta decay, as seen in the equation Recall that beta decay is when a beta particle is ejected from an atom. In order to accelerate away from the nucleus, the particle must be acted on by a force. Enrico Fermi was the first to envision this type of force. While this force is appropriately labeled, it remains stronger than the gravitational force. However, its range is even smaller than that of the strong force, as can be seen in Table 23.1. The weak nuclear force is more important than it may appear at this time, as will be addressed when we discuss quarks.
| Force | Approximate Relative Strength[1] | Range |
|---|---|---|
| [1]Relative strength is based on the strong force felt by a proton–proton pair. | ||
| Gravity | ||
| Weak | ||
| Electromagnetic | ||
| Strong | 1 | |
Transmitting the Four Fundamental Forces
Transmitting the Four Fundamental Forces
Just as it troubled Einstein prior to formulating the gravitational field theory, the concept of forces acting over a distance had greatly troubled particle physicists. That is, how does one proton know that another exists? Furthermore, what causes one proton to make a second proton repel? Or, for that matter, what is it about a proton that causes a neutron to attract? These mysterious interactions were first considered by Hideki Yukawa in 1935 and laid the foundation for much of what we now understand about particle physics.
Hideki Yukawa’s focus was on the strong nuclear force and, in particular, its incredibly short range. His idea was a blend of particles, relativity, and quantum mechanics that was applicable to all four forces. Yukawa proposed that the nuclear force is actually transmitted by the exchange of particles, called carrier particles, and that what we commonly refer to as the force’s field consists of these carrier particles. Specifically for the strong nuclear force, Yukawa proposed that a previously unknown particle, called a pion, is exchanged between nucleons, transmitting the force between them. Figure 23.3 illustrates how a pion would carry a force between a proton and a neutron.
In Yukawa’s strong force, the carrier particle is assumed to be transmitted at the speed of light and is continually transferred between the two nucleons shown. The particle that Yukawa predicted was finally discovered within cosmic rays in 1947. Its name, the pion, stands for pi meson, where meson means medium mass; it’s a medium mass because it is smaller than a nucleon but larger than an electron. Yukawa launched the field that is now called quantum chromodynamics, and the carrier particles are now called gluons due to their strong binding power. The reason for the change in the particle name will be explained when quarks are discussed later in this section.
As you may assume, the strong force is not the only force with a carrier particle. Nuclear decay from the weak force also requires a particle transfer. In the weak force are the following three: the weak negative carrier, W–; the weak positive carrier, W+; and the zero charge carrier, Z0. As we will see, Fermi inferred that these particles must carry mass, as the total mass of the products of nuclear decay is slightly larger than the total mass of all reactants after nuclear decay.
The carrier particle for the electromagnetic force is, not surprisingly, the photon. After all, just as a lightbulb can emit photons from a charged tungsten filament, the photon can be used to transfer information from one electrically charged particle to another. Finally, the graviton is the proposed carrier particle for gravity. While it has not yet been found, scientists are currently looking for evidence of its existence (see Boundless Physics: Searching for the Graviton).
So how does a carrier particle transmit a fundamental force? Figure 23.4 shows a virtual photon transmitted from one positively charged particle to another. The transmitted photon is referred to as a virtual particle because it cannot be directly observed while transmitting the force. Figure 23.5 shows a way of graphing the exchange of a virtual photon between the two positively charged particles. This graph of time versus position is called a Feynman diagram, after the brilliant American physicist Richard Feynman (1918–1988), who developed it.
The Feynman diagram should be read from the bottom up to show the movement of particles over time. In it, you can see that the left proton is propelled leftward from the photon emission, while the right proton feels an impulse to the right when the photon is received. In addition to the Feynman diagram, Richard Feynman was one of the theorists who developed the field of quantum electrodynamics (QED), which further describes electromagnetic interactions on the submicroscopic scale. For this work, he shared the 1965 Nobel Prize with Julian Schwinger and S.I. Tomonaga. A Feynman diagram explaining the strong force interaction hypothesized by Yukawa can be seen in Figure 23.6. Here, you can see the change in particle type due to the exchange of the pi meson.
The relative masses of the listed carrier particles describe something valuable about the four fundamental forces, as can be seen in Table 23.2. W bosons (consisting of and bosons) and Z bosons ( bosons), carriers of the weak nuclear force, are nearly 1,000 times more massive than pions, carriers of the strong nuclear force. Simultaneously, the distance that the weak nuclear force can be transmitted is approximately times the strong force transmission distance. Unlike carrier particles, which have a limited range, the photon is a massless particle that has no limit to the transmission distance of the electromagnetic force. This relationship leads scientists to understand that the yet-unfound graviton is likely massless as well.
| Force | Carrier Particle | Range | Relative Strength[1] |
|---|---|---|---|
| [1]Relative strength is based on the strong force felt by a proton-proton pair. | |||
| Gravity | Graviton (theorized) | ||
| Weak | W and Z bosons | ||
| Electromagnetic | Photon | ||
| Strong | Pi mesons or pions (now known as gluons) | 1 | |
Boundless Physics
Searching for the Graviton
From Newton’s Universal Law of Gravitation to Einstein’s field equations, gravitation has held the focus of scientists for centuries. Given the discovery of carrier particles during the twentieth century, the importance of understanding gravitation has yet again gained the interest of prominent physicists everywhere.
With carrier particles discovered for three of the four fundamental forces, it is sensible to scientists that a similar particle, titled the graviton, must exist for the gravitational force. While evidence of this particle is yet to be uncovered, scientists are working diligently to discover its existence.
So what do scientists think about the unfound particle? For starters, the graviton (like the photon) should be a massless particle traveling at the speed of light. This is assumed because, like the electromagnetic force, gravity is an inverse square law, . Scientists also theorize that the graviton is an electrically neutral particle, as an empty space within the influence of gravity is chargeless.
However, because gravity is such a weak force, searching for the graviton has resulted in some unique methods. LIGO, the Laser Interferometer Gravitational-Wave Observatory, is one tool currently being utilized (see Figure 23.7). While searching for a gravitational wave to find a carrier particle may seem counterintuitive, it is similar to the approach taken by Planck and Einstein to learn more about the photon. According to wave-particle duality, if a gravitational wave can be found, the graviton should be present along with it. Predicted by Einstein’s theory of general relativity, scientists have been monitoring binary star systems for evidence of these gravitational waves.
Particle accelerators like the Large Hadron Collider (LHC) are being used to search for the graviton through high-energy collisions. While scientists at the LHC speculate that the particle may not exist long enough to be seen, evidence of its prior existence, like footprints in the sand, can be found through gaps in projected energy and momentum.
Some scientists are even searching the remnants of the Big Bang in an attempt to find the graviton. By observing the cosmic background radiation, they are looking for anomalies in gravitational waves that would provide information about the gravity particles that existed at the start of our universe.
Regardless of the method used, scientists should know the graviton once they find it. A massless, chargeless particle with a spin of 2 and traveling at the speed of light—there is no other particle like it. Should it be found, its discovery would surely be considered by future generations to be on par with those of Newton and Einstein.
- Binary star systems have high temperature.
- Binary star systems have low density.
- Binary star systems contain a large amount of mass, but because they are orbiting each other, the gravitational field between the two is much less.
- Binary star systems contain a large amount of mass. As a result, the gravitational field between the two is great.
Accelerators Create Matter From Energy
Accelerators Create Matter From Energy
Before looking at all the particles that make up our universe, let us first examine some of the machines that create them. The fundamental process in creating unknown particles is to accelerate known particles, such as protons or electrons, and direct a beam of them toward a target. Collisions with target nuclei provide a wealth of information, such as information obtained by Rutherford in the gold foil experiment. If the energy of the incoming particles is large enough, new matter can even be created in the collision. The more energy input or ΔE, the more matter m can be created, according to mass energy equivalence . Limitations are placed on what can occur by known conservation laws, such as conservation of mass-energy, momentum, and charge. Even more interesting are the unknown limitations provided by nature. While some expected reactions do occur, others do not, and still other unexpected reactions may appear. New laws are revealed, and the vast majority of what we know about particle physics has come from accelerator laboratories. It is the particle physicist’s favorite indoor sport.
Our earliest model of a particle accelerator comes from the Van de Graaff generator. The relatively simple device, which you have likely seen in physics demonstrations, can be manipulated to produce potentials as great as 50 million volts. While these machines do not have energies large enough to produce new particles, analysis of their accelerated ions was instrumental in exploring several aspects of the nucleus.
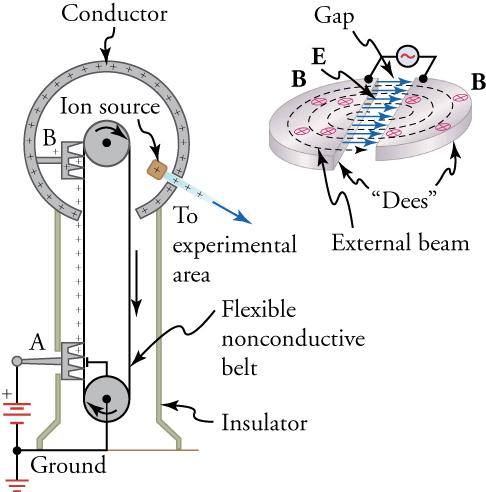
Another equally famous early accelerator is the cyclotron, invented in 1930 by the American physicist, E.O. Lawrence (1901–1958). Figure 23.8 is a visual representation with more detail. Cyclotrons use fixed-frequency alternating electric fields to accelerate particles. The particles spiral outward in a magnetic field, making increasingly larger radius orbits during acceleration. This clever arrangement allows the successive addition of electric potential energy with each loop. As a result, greater particle energies are possible than in a Van de Graaff generator.
A synchrotron is a modification of the cyclotron in which particles continually travel in a fixed-radius orbit, increasing speed each time. Accelerating voltages are synchronized with the particles to accelerate them, hence the name. Additionally, magnetic field strength is increased to keep the orbital radius constant as energy increases. A ring of magnets and accelerating tubes, as shown in Figure 23.9, are the major components of synchrotrons. High-energy particles require strong magnetic fields to steer them, so superconducting magnets are commonly employed. Still limited by achievable magnetic field strengths, synchrotrons need to be very large at very high energies since the radius of a high-energy particle’s orbit is very large.
To further probe the nucleus, physicists need accelerators of greater energy and detectors of shorter wavelength. To do so requires not only greater funding but greater ingenuity as well. Colliding beams used at both the Fermi National Accelerator Laboratory (Fermilab; see Figure 23.10) near Chicago and the LHC in Switzerland are designed to reduce energy loss in particle collisions. Typical stationary particle detectors lose a large amount of energy to the recoiling target struck by the accelerating particle. By providing head-on collisions between particles moving in opposite directions, colliding beams make it possible to create particles with momenta and kinetic energies near zero. This allows for particles of greater energy and mass to be created. Figure 23.11 is a schematic representation of this effect. In addition to circular accelerators, linear accelerators can be used to reduce energy radiation losses. The Stanford Linear Accelerator Center (now called the SLAC National Accelerator Laboratory) in California is home to the largest such accelerator in the world.
>
Check Your Understanding
Check Your Understanding
Which of the four forces is responsible for radioactive decay?
- the electromagnetic force
- the gravitational force
- the strong nuclear force
- the weak nuclear force
What force or forces exist between an electron and a proton?
- the strong nuclear force, the electromagnetic force, and gravity
- the weak nuclear force, the strong nuclear force, and gravity
- the weak nuclear force, the strong nuclear force, and the electromagnetic force
- the weak nuclear force, the electromagnetic force, and gravity
What is the proposed carrier particle for the gravitational force?
- boson
- graviton
- gluon
- photon
- Range of a carrier particle is inversely proportional to its mass.
- Range of a carrier particle is inversely proportional to square of its mass.
- Range of a carrier particle is directly proportional to its mass.
- Range of a carrier particle is directly proportional to square of its mass.
What type of particle accelerator uses fixed-frequency oscillating electric fields to accelerate particles?
- cyclotron
- synchrotron
- betatron
- Van de Graaff accelerator
- A constant magnetic force is exerted on particles at all radii. As the radius increases, the velocity of the particle must increase to maintain this constant force.
- A constant centripetal force is exerted on particles at all radii. As the radius increases, the velocity of the particle must decrease to maintain this constant force.
- A constant magnetic force is exerted on particles at all radii. As the radius increases, the velocity of the particle must decrease to maintain this constant force.
- A constant centripetal force is exerted on particles at all radii. As the radius increases, the velocity of the particle must increase to maintain this constant force.
Which of the four forces is responsible for the structure of galaxies?
- electromagnetic force
- gravity
- strong nuclear force
- weak nuclear force