Learning Objectives
Learning Objectives
By the end of this section, you will be able to do the following:
- Explain the meaning of slope in position vs. time graphs
- Solve problems using position vs. time graphs
| dependent variable | independent variable | tangent |
Graphing Position as a Function of Time
Graphing Position as a Function of Time
A graph, like a picture, is worth a thousand words. Graphs not only contain numerical information, they also reveal relationships between physical quantities. In this section, we will investigate kinematics by analyzing graphs of position over time.
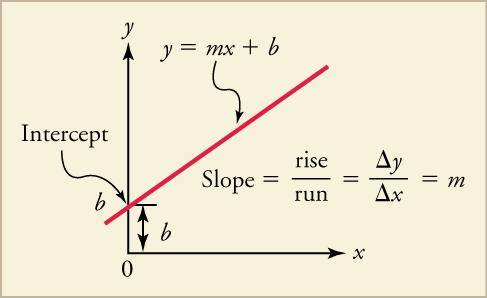
Graphs in this text have perpendicular axes, one horizontal and the other vertical. When two physical quantities are plotted against each other, the horizontal axis is usually considered the independent variable, and the vertical axis is the dependent variable. In algebra, you would have referred to the horizontal axis as the x-axis and the vertical axis as the y-axis. As in Figure 2.11, a straight-line graph has the general form .
Here m is the slope, defined as the rise divided by the run (as seen in the figure) of the straight line. The letter b is the y-intercept which is the point at which the line crosses the vertical, y-axis. In terms of a physical situation in the real world, these quantities will take on a specific significance, as we will see below. (Figure 2.11.)
In physics, time is usually the independent variable. Other quantities, such as displacement, are said to depend upon it. A graph of position versus time, therefore, would have position on the vertical axis (dependent variable) and time on the horizontal axis (independent variable). In this case, to what would the slope and y-intercept refer? Let’s look back at our original example when studying distance and displacement.
The drive to school was 5 km from home. Let’s assume it took 10 minutes to make the drive and that your parent was driving at a constant velocity the whole time. The position versus time graph for this section of the trip would look like that shown in Figure 2.12.
As we said before, d0 = 0 because we call home our O and start calculating from there. In Figure 2.12, the line starts at d = 0, as well. This is the b in our equation for a straight line. Our initial position in a position versus time graph is always the place where the graph crosses the x-axis at t = 0. What is the slope? The rise is the change in position, (i.e., displacement) and the run is the change in time. This relationship can also be written
This relationship was how we defined average velocity. Therefore, the slope in a d versus t graph, is the average velocity.
Tips For Success
Sometimes, as is the case where we graph both the trip to school and the return trip, the behavior of the graph looks different during different time intervals. If the graph looks like a series of straight lines, then you can calculate the average velocity for each time interval by looking at the slope. If you then want to calculate the average velocity for the entire trip, you can do a weighted average.
Let’s look at another example. Figure 2.13 shows a graph of position versus time for a jet-powered car on a very flat dry lake bed in Nevada.
Using the relationship between dependent and independent variables, we see that the slope in the graph in Figure 2.13 is average velocity, vavg and the intercept is displacement at time zero—that is, d0. Substituting these symbols into y = mx + b gives
or
Thus a graph of position versus time gives a general relationship among displacement, velocity, and time, as well as giving detailed numerical information about a specific situation. From the figure we can see that the car has a position of 400 m at t = 0 s, 650 m at t = 1.0 s, and so on. And we can learn about the object’s velocity, as well.
Snap Lab
Graphing Motion
In this activity, you will release a ball down a ramp and graph the ball’s displacement vs. time.
- Choose an open location with lots of space to spread out so there is less chance for tripping or falling due to rolling balls.
- 1 ball
- 1 board
- 2 or 3 books
- 1 stopwatch
- 1 tape measure
- 6 pieces of masking tape
- 1 piece of graph paper
- 1 pencil
- Build a ramp by placing one end of the board on top of the stack of books. Adjust location, as necessary, until there is no obstacle along the straight line path from the bottom of the ramp until at least the next 3 m.
- Mark distances of 0.5 m, 1.0 m, 1.5 m, 2.0 m, 2.5 m, and 3.0 m from the bottom of the ramp. Write the distances on the tape.
- Have one person take the role of the experimenter. This person will release the ball from the top of the ramp. If the ball does not reach the 3.0 m mark, then increase the incline of the ramp by adding another book. Repeat this Step as necessary.
- Have the experimenter release the ball. Have a second person, the timer, begin timing the trial once the ball reaches the bottom of the ramp and stop the timing once the ball reaches 0.5 m. Have a third person, the recorder, record the time in a data table.
- Repeat Step 4, stopping the times at the distances of 1.0 m, 1.5 m, 2.0 m, 2.5 m, and 3.0 m from the bottom of the ramp.
- Use your measurements of time and the displacement to make a position vs. time graph of the ball’s motion.
- Repeat Steps 4 through 6, with different people taking on the roles of experimenter, timer, and recorder. Do you get the same measurement values regardless of who releases the ball, measures the time, or records the result? Discuss possible causes of discrepancies, if any.
- True
- False
Solving Problems Using Position vs. Time Graphs
So how do we use graphs to solve for things we want to know like velocity?
Worked Example
Using Position–Time Graph to Calculate Average Velocity: Jet Car
Find the average velocity of the car whose position is graphed in Figure 1.13.
Strategy
The slope of a graph of d vs. t is average velocity, since slope equals rise over run.
Since the slope is constant here, any two points on the graph can be used to find the slope.
- Choose two points on the line. In this case, we choose the points labeled on the graph: (6.4 s, 2000 m) and (0.50 s, 525 m). (Note, however, that you could choose any two points.)
- Substitute the d and t values of the chosen points into the equation. Remember in calculating change (Δ) we always use final value minus initial value.
2.8
This is an impressively high land speed (900 km/h, or about 560 mi/h): much greater than the typical highway speed limit of 27 m/s or 96 km/h, but considerably shy of the record of 343 m/s or 1,234 km/h, set in 1997.
But what if the graph of the position is more complicated than a straight line? What if the object speeds up or turns around and goes backward? Can we figure out anything about its velocity from a graph of that kind of motion? Let’s take another look at the jet-powered car. The graph in Figure 2.14 shows its motion as it is getting up to speed after starting at rest. Time starts at zero for this motion (as if measured with a stopwatch), and the displacement and velocity are initially 200 m and 15 m/s, respectively.
The graph of position versus time in Figure 2.14 is a curve rather than a straight line. The slope of the curve becomes steeper as time progresses, showing that the velocity is increasing over time. The slope at any point on a position-versus-time graph is the instantaneous velocity at that point. It is found by drawing a straight line tangent to the curve at the point of interest and taking the slope of this straight line. Tangent lines are shown for two points in Figure 2.14. The average velocity is the net displacement divided by the time traveled.
Worked Example
Using Position–Time Graph to Calculate Average Velocity: Jet Car, Take Two
Calculate the instantaneous velocity of the jet car at a time of 25 s by finding the slope of the tangent line at point Q in this figure.
Strategy
The slope of a curve at a point is equal to the slope of a straight line tangent to the curve at that point.
- Find the tangent line to the curve at .
- Determine the endpoints of the tangent. These correspond to a position of 1,300 m at time 19 s and a position of 3120 m at time 32 s.
- Plug these endpoints into the equation to solve for the slope, v.
2.9
The entire graph of v versus t can be obtained in this fashion.
Practice Problems
Practice Problems
Calculate the average velocity of the object shown in the graph below over the whole time interval.
- 0.25 m/s
- 0.31 m/s
- 3.2 m/s
- 4.00 m/s
 True or False: By taking the slope of the curve in the graph you can verify that the velocity of the jet car is at .
True or False: By taking the slope of the curve in the graph you can verify that the velocity of the jet car is at .- True
- False
Check Your Understanding
Check Your Understanding
Which of the following information about motion can be determined by looking at a position vs. time graph that is a straight line?
- frame of reference
- average acceleration
- velocity
- direction of force applied
- True
- False