Learning Objectives
Learning Objectives
By the end of this section, you will be able to do the following:
- Describe Rutherford’s experiment and his model of the atom
- Describe emission and absorption spectra of atoms
- Describe the Bohr model of the atom
- Calculate the energy of electrons when they change energy levels
- Calculate the frequency and wavelength of emitted photons when electrons change energy levels
- Describe the quantum model of the atom
| energy-level diagram | excited state | Fraunhofer lines |
| ground state | Heisenberg Uncertainty Principle | hydrogen-like atoms |
| planetary model of the atom | Rutherford scattering | Rydberg constant |
How do we know that atoms are really there if we cannot see them with our own eyes? While often taken for granted, our knowledge of the existence and structure of atoms is the result of centuries of contemplation and experimentation. The earliest known speculation on the atom dates back to the fifth century B.C., when Greek philosophers Leucippus and Democritus contemplated whether a substance could be divided without limit into ever smaller pieces. Since then, scientists such as John Dalton (1766–1844), Amadeo Avogadro (1776–1856), and Dmitri Mendeleev (1834–1907) helped to discover the properties of that fundamental structure of matter. While much could be written about any number of important scientific philosophers, this section will focus on the role played by Ernest Rutherford (1871–1937). Though his understanding of our most elemental matter is rooted in the success of countless prior investigations, his surprising discovery about the interior of the atom is most fundamental in explaining so many well-known phenomena.
Rutherford’s Experiment
Rutherford’s Experiment
In the early 1900’s, the plum pudding model was the accepted model of the atom. Proposed in 1904 by J. J. Thomson, the model suggested that the atom was a spherical ball of positive charge, with negatively charged electrons scattered evenly throughout. In that model, the positive charges made up the pudding, while the electrons acted as isolated plums. During its short life, the model could be used to explain why most particles were neutral, although with an unbalanced number of plums, electrically charged atoms could exist.
When Ernest Rutherford began his gold foil experiment in 1909, it is unlikely that anyone would have expected that the plum pudding model would be challenged. However, using a radioactive source, a thin sheet of gold foil, and a phosphorescent screen, Rutherford would uncover something so great that he would later call it “the most incredible event that has ever happened to me in my life”[James, L. K. (1993). Nobel Laureates in Chemistry, 1901–1992. Washington, DC: American Chemical Society.]
The experiment that Rutherford designed is shown in Figure 22.2. As you can see in, a radioactive source was placed in a lead container with a hole in one side to produce a beam of positively charged helium particles, called alpha particles. Then, a thin gold foil sheet was placed in the beam. When the high-energy alpha particles passed through the gold foil, they were scattered. The scattering was observed from the bright spots they produced when they struck the phosphor screen.
The expectation of the plum pudding model was that the high-energy alpha particles would be scattered only slightly by the presence of the gold sheet. Because the energy of the alpha particles was much higher than those typically associated with atoms, the alpha particles should have passed through the thin foil much like a supersonic bowling ball would crash through a few dozen rows of bowling pins. Any deflection was expected to be minor, and due primarily to the electrostatic Coulomb force between the alpha particles and the foil’s interior electric charges.
However, the true result was nothing of the sort. While the majority of alpha particles passed through the foil unobstructed, Rutherford and his collaborators Hans Geiger and Ernest Marsden found that alpha particles occasionally were scattered to large angles, and some even came back in the direction from which they came! The result, called Rutherford scattering, implied that the gold nuclei were actually very small when compared with the size of the gold atom. As shown in Figure 22.3, the dense nucleus is surrounded by mostly empty space of the atom, an idea verified by the fact that only 1 in 8,000 particles was scattered backward.
Although the results of the experiment were published by his colleagues in 1909, it took Rutherford two years to convince himself of their meaning. Rutherford later wrote: “It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you. On consideration, I realized that this scattering backwards ... [meant] ... the greatest part of the mass of the atom was concentrated in a tiny nucleus.” In 1911, Rutherford published his analysis together with a proposed model of the atom, which was in part based on Geiger’s work from the previous year. As a result of the paper, the size of the nucleus was determined to be about m, or 100,000 times smaller than the atom. That implies a huge density, on the order of g/cm3, much greater than any macroscopic matter.
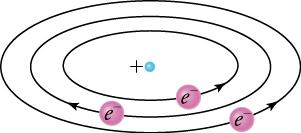
Based on the size and mass of the nucleus revealed by his experiment, as well as the mass of electrons, Rutherford proposed the planetary model of the atom. The planetary model of the atom pictures low-mass electrons orbiting a large-mass nucleus. The sizes of the electron orbits are large compared with the size of the nucleus, and most of the atom is a vacuum. The model is analogous to how low-mass planets in our solar system orbit the large-mass Sun. In the atom, the attractive Coulomb force is analogous to gravitation in the planetary system (see Figure 22.4).
Virtual Physics
Rutherford Scattering
How did Rutherford figure out the structure of the atom without being able to see it? Explore the answer through this simulation of the famous experiment in which he disproved the plum pudding model by observing alpha particles bouncing off atoms and determining that they must have a small core.
Tips For Success
As you progress through the model of the atom, consider the effect that experimentation has on the scientific process. Ask yourself the following: What would our model of the atom be without Rutherford’s gold foil experiment? What further understanding of the atom would not have been gained? How would that affect our current technologies? Though often confusing, experiments taking place today to further understand composition of the atom could perhaps have a similar effect.
Absorption and Emission Spectra
Absorption and Emission Spectra
In 1900, Max Planck recognized that all energy radiated from a source is emitted by atoms in quantum states. How would that radical idea relate to the interior of an atom? The answer was first found by investigating the spectrum of light or emission spectrum produced when a gas is highly energized.
Figure 22.6 shows how to isolate the emission spectrum of one such gas. The gas is placed in the discharge tube at the left, where it is energized to the point at which it begins to radiate energy or emit light. The radiated light is channeled by a thin slit and then passed through a diffraction grating, which will separate the light into its constituent wavelengths. The separated light will then strike the photographic film on the right.
The line spectrum shown in part (b) of Figure 22.6 is the output shown on the film for excited iron. Note that this spectrum is not continuous but discrete. In other words, only particular wavelengths are emitted by the iron source. Why would that be the case?
The spectrum of light created by excited iron shows a variety of discrete wavelengths emitted within the visible spectrum. Each element, when excited to the appropriate degree, will create a discrete emission spectrum as in part (b) of Figure 22.6. However, the wavelengths emitted will vary from element to element. The emission spectrum for iron was chosen for Figure 22.6 solely because a substantial portion of its emission spectrum is within the visible spectrum. Figure 22.7 shows the emission spectrum for hydrogen. Note that, while discrete, a large portion of hydrogen emission takes place in the ultraviolet and infrared regions.
Just as an emission spectrum shows all discrete wavelengths emitted by a gas, an absorption spectrum will show all light that is absorbed by a gas. Black lines exist where the wavelengths are absorbed, with the remainder of the spectrum lit by light is free to pass through. What relationship do you think exists between the black lines of a gas’s absorption spectrum and the colored lines of its emission spectrum? Figure 22.8 shows the absorption spectrum of the Sun. The black lines are called Fraunhofer lines, and they correspond to the wavelengths absorbed by gases in the Sun’s exterior.
Bohr’s Explanation of the Hydrogen Spectrum
Bohr’s Explanation of the Hydrogen Spectrum
To tie the unique signatures of emission spectra to the composition of the atom itself would require clever thinking. Niels Bohr (1885–1962), a Danish physicist, did just that, by making immediate use of Rutherford’s planetary model of the atom. Bohr, shown in Figure 22.9, became convinced of its validity and spent part of 1912 at Rutherford’s laboratory. In 1913, after returning to Copenhagen, he began publishing his theory of the simplest atom, hydrogen, based on Rutherford’s planetary model.
Bohr was able to derive the formula for the hydrogen spectrum using basic physics, the planetary model of the atom, and some very important new conjectures. His first conjecture was that only certain orbits are allowed: In other words, in an atom, the orbits of electrons are quantized. Each quantized orbit has a different distinct energy, and electrons can move to a higher orbit by absorbing energy or drop to a lower orbit by emitting energy. Because of the quantized orbits, the amount of energy emitted or absorbed must also be quantized, producing the discrete spectra seen in Figure 22.6 and Figure 22.8. In equation form, the amount of energy absorbed or emitted can be found as
where refers to the energy of the initial quantized orbit, and refers to the energy of the final orbits. Furthermore, the wavelength emitted can be found using the equation
and relating the wavelength to the frequency found using the equation , where v corresponds to the speed of light.
It makes sense that energy is involved in changing orbits. For example, a burst of energy is required for a satellite to climb to a higher orbit. What is not expected is that atomic orbits should be quantized. Quantization is not observed for satellites or planets, which can have any orbit, given the proper energy (see Figure 22.10).
Figure 22.11 shows an energy-level diagram, a convenient way to display energy states. Each of the horizontal lines corresponds to the energy of an electron in a different orbital. Energy is plotted vertically with the lowest or ground state at the bottom and with excited states above. The vertical arrow downwards shows energy being emitted out of the atom due to an electron dropping from one excited state to another. That would correspond to a line shown on the atom’s emission spectrum. The Lyman series shown in Figure 22.7 results from electrons dropping to the ground state, while the Balmer and Paschen series result to electrons dropping to the n = 2 and n = 3 states, respectively.
Energy and Wavelength of Emitted Hydrogen Spectra
Energy and Wavelength of Emitted Hydrogen Spectra
The energy associated with a particular orbital of a hydrogen atom can be found using the equation
where n corresponds to the orbital value from the atom’s nucleus. The negative value in the equation is based upon a baseline energy of zero when the electron is infinitely far from the atom. As a result, the negative value shows that energy is necessary to free the electron from its orbital state. The minimum energy to free the electron is also referred to as its binding energy. The equation is only valid for atoms with single electrons in their orbital shells (like hydrogen). For ionized atoms similar to hydrogen, the following formula may be used.
Please note that corresponds to –13.6 eV, as mentioned earlier. Additionally, refers to the atomic number of the element studied. The atomic number is the number of protons in the nucleus—it is different for each element. The above equation is derived from some basic physics principles, namely conservation of energy, conservation of angular momentum, Coulomb’s law, and centripetal force. There are three derivations that result in the orbital energy equations, and they are shown below. While you can use the energy equations without understanding the derivations, they will help to remind you of just how valuable those fundamental concepts are.
Derivation 1 (Finding the Radius of an Orbital)
One primary difference between the planetary model of the solar system and the planetary model of the atom is the cause of the circular motion. While gravitation causes the motion of orbiting planets around an interior star, the Coulomb force is responsible for the circular shape of the electron’s orbit. The magnitude of the centripetal force is , while the magnitude of the Coulomb force is . The assumption here is that the nucleus is more massive than the stationary electron, and the electron orbits about it. That is consistent with the planetary model of the atom. Equating the Coulomb force and the centripetal force,
which yields
Derivation 2 (Finding the Velocity of the Orbiting Electron)
Bohr was clever enough to find a way to calculate the electron orbital energies in hydrogen. That was an important first step that has been improved upon, but it is well worth repeating here, because it does correctly describe many characteristics of hydrogen. Assuming circular orbits, Bohr proposed that the angular momentum L of an electron in its orbit is also quantized, that is, it has only specific, discrete values. The value for L is given by the formula
where L is the angular momentum, me is the electron’s mass, rn is the radius of the n th orbit, and h is Planck’s constant. Note that angular momentum is . For a small object at a radius r, , and , so that Quantization says that the value of mvr can only be equal to h / 2, 2h / 2, 3h / 2 , etc. At the time, Bohr himself did not know why angular momentum should be quantized, but by using that assumption, he was able to calculate the energies in the hydrogen spectrum, something no one else had done at the time.
Derivation 3 (Finding the Energy of the Orbiting Electron)
To get the electron orbital energies, we start by noting that the electron energy is the sum of its kinetic and potential energy.
Kinetic energy is the familiar , assuming the electron is not moving at a relativistic speed. Potential energy for the electron is electrical, or , where V is the potential due to the nucleus, which looks like a point charge. The nucleus has a positive charge ; thus, , recalling an earlier equation for the potential due to a point charge from the chapter on Electricity and Magnetism. Since the electron’s charge is negative, we see that Substituting the expressions for KE and PE,
Now we solve for rn and v using the equation for angular momentum , giving
and
Substituting the expression for rn and v into the above expressions for energy (KE and PE), and performing algebraic manipulation, yields
for the orbital energies of hydrogen-like atoms. Here, Eo is the ground-state energy (n = 1) for hydrogen (Z = 1) and is given by
Thus, for hydrogen,
The relationship between orbital energies and orbital states for the hydrogen atom can be seen in Figure 22.12.
Worked Example
A hydrogen atom is struck by a photon. How much energy must be absorbed from the photon to raise the electron of the hydrogen atom from its ground state to its second orbital?
Strategy
The hydrogen atom has an atomic number of Z = 1. Raising the electron from the ground state to its second orbital will increase its orbital level from n = 1 to n = 2. The energy determined will be measured in electron-volts.
The amount of energy necessary to cause the change in electron state is the difference between the final and initial energies of the electron. The final energy state of the electron can be found using
Knowing the n and Z values for the hydrogen atom, and knowing that Eo = –13.6 eV, the result is
The original amount of energy associated with the electron is equivalent to the ground state orbital, or
The amount of energy necessary to change the orbital state of the electron can be found by determining the electron’s change in energy.
The energy required to change the orbital state of the electron is positive. That means that for the electron to move to a state with greater energy, energy must be added to the atom. Should the electron drop back down to its original energy state, a change of –10.2 eV would take place, and 10.2 eV of energy would be emitted from the atom. Just as only quantum amounts of energy may be absorbed by the atom, only quantum amounts of energy can be emitted from the atom. That helps to explain many of the quantum light effects that you have learned about previously.
Worked Example
Characteristic X-Ray Energy
Calculate the approximate energy of an X-ray emitted for an n = 2 to n = 1 transition in a tungsten anode in an X-ray tube.
Strategy
How do we calculate energies in a multiple-electron atom? In the case of characteristic X-rays, the following approximate calculation is reasonable. Characteristic X-rays are produced when an inner-shell vacancy is filled. Inner-shell electrons are nearer the nucleus than others in an atom and thus feel little net effect from the others. That is similar to what happens inside a charged conductor, where its excess charge is distributed over the surface so that it produces no electric field inside. It is reasonable to assume the inner-shell electrons have hydrogen-like energies, as given by
For tungsten, Z = 74, so that the effective charge is 73.
The amount of energy given off as an X-ray is found using
where
and
Thus,
This large photon energy is typical of characteristic X-rays from heavy elements. It is large compared with other atomic emissions because it is produced when an inner-shell vacancy is filled, and inner-shell electrons are tightly bound. Characteristic X-ray energies become progressively larger for heavier elements because their energy increases approximately as Z2. Significant accelerating voltage is needed to create such inner-shell vacancies, because other shells are filled and you cannot simply bump one electron to a higher filled shell. You must remove it from the atom completely. In the case of tungsten, at least 72.5 kV is needed. Tungsten is a common anode material in X-ray tubes; so much of the energy of the impinging electrons is absorbed, raising its temperature, that a high-melting-point material like tungsten is required.
The wavelength of light emitted by an atom can also be determined through basic derivations. Let us consider the energy of a photon emitted from a hydrogen atom in a downward transition, given by the equation
Substituting , we get
Dividing both sides of the equation by hc gives us an expression for ,
It can be shown that
where R is the Rydberg constant.
Simplified, the formula for determining emitted wavelength can now be written as
Worked Example
What wavelength of light is emitted by an electron dropping from the third orbital to the ground state of a hydrogen atom?
Strategy
The ground state of a hydrogen atom is considered the first orbital of the atom. As a result, nf = 1 and ni = 3. The Rydberg constant has already been determined and will be constant regardless of atom chosen.
For the equation above, calculate wavelength based on the known energy states.
Rearranging the equation for wavelength yields
This wavelength corresponds to light in the ultraviolet spectrum. As a result, we would not be able to see the photon of light emitted when an electron drops from its third to first energy state. However, it is worth noting that by supplying light of wavelength precisely 102.6 nm, we can cause the electron in hydrogen to move from its first to its third orbital state.
Limits of Bohr’s Theory and the Quantum Model of the Atom
Limits of Bohr’s Theory and the Quantum Model of the Atom
There are limits to Bohr’s theory. It does not account for the interaction of bound electrons, so it cannot be fully applied to multielectron atoms, even one as simple as the two-electron helium atom. Bohr’s model is what we call semiclassical. The orbits are quantized (nonclassical) but are assumed to be simple circular paths (classical). As quantum mechanics was developed, it became clear that there are no well-defined orbits; rather, there are clouds of probability. Additionally, Bohr’s theory did not explain that some spectral lines are doublets or split into two when examined closely. While we shall examine a few of those aspects of quantum mechanics in more detail, it should be kept in mind that Bohr did not fail. Rather, he made very important steps along the path to greater knowledge and laid the foundation for all of atomic physics that has since evolved.
DeBroglie’s Waves
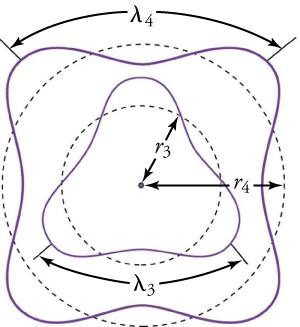
Following Bohr’s initial work on the hydrogen atom, a decade was to pass before Louis de Broglie proposed that matter has wave properties. The wave-like properties of matter were subsequently confirmed by observations of electron interference when scattered from crystals. Electrons can exist only in locations where they interfere constructively. How does that affect electrons in atomic orbits? When an electron is bound to an atom, its wavelength must fit into a small space, something like a standing wave on a string (see Figure 22.13). Orbits in which an electron can constructively interfere with itself are allowed. All orbits in which constructive interference cannot occur are not able to exist. Thus, only certain orbits are allowed. The wave nature of an electron, according to de Broglie, is why the orbits are quantized!
For a circular orbit, constructive interference occurs when the electron’s wavelength fits neatly into the circumference, so that wave crests always align with crests and wave troughs align with troughs, as shown in Figure 22.13(b). More precisely, when an integral multiple of the electron’s wavelength equals the circumference of the orbit, constructive interference is obtained. In equation form, the condition for constructive interference and an allowed electron orbit is
where is the electron’s wavelength and rn is the radius of that circular orbit. Figure 22.14 shows the third and fourth orbitals of a hydrogen atom.
Heisenberg Uncertainty
How does determining the location of an electron change its trajectory? The answer is fundamentally important—measurement affects the system being observed. It is impossible to measure a physical quantity exactly, and greater precision in measuring one quantity produces less precision in measuring a related quantity. It was Werner Heisenberg who first stated that limit to knowledge in 1929 as a result of his work on quantum mechanics and the wave characteristics of all particles (see Figure 22.15).
For example, you can measure the position of a moving electron by scattering light or other electrons from it. However, by doing so, you are giving the electron energy, and therefore imparting momentum to it. As a result, the momentum of the electron is affected and cannot be determined precisely. This change in momentum could be anywhere from close to zero up to the relative momentum of the electron (). Note that, in this case, the particle is an electron, but the principle applies to any particle.
Viewing the electron through the model of wave-particle duality, Heisenberg recognized that, because a wave is not located at one fixed point in space, there is an uncertainty associated with any electron’s position. That uncertainty in position, , is approximately equal to the wavelength of the particle. That is, . There is an interesting trade-off between position and momentum. The uncertainty in an electron’s position can be reduced by using a shorter-wavelength electron, since . But shortening the wavelength increases the uncertainty in momentum, since . Conversely, the uncertainty in momentum can be reduced by using a longer-wavelength electron, but that increases the uncertainty in position. Mathematically, you can express the trade-off by multiplying the uncertainties. The wavelength cancels, leaving
Therefore, if one uncertainty is reduced, the other must increase so that their product is . With the use of advanced mathematics, Heisenberg showed that the best that can be done in a simultaneous measurement of position and momentum is
That relationship is known as the Heisenberg uncertainty principle.
The Quantum Model of the Atom
Because of the wave characteristic of matter, the idea of well-defined orbits gives way to a model in which there is a cloud of probability, consistent with Heisenberg’s uncertainty principle. Figure 22.16 shows how the principle applies to the ground state of hydrogen. If you try to follow the electron in some well-defined orbit using a probe that has a wavelength small enough to measure position accurately, you will instead knock the electron out of its orbit. Each measurement of the electron’s position will find it to be in a definite location somewhere near the nucleus. Repeated measurements reveal a cloud of probability like that in the figure, with each speck the location determined by a single measurement. There is not a well-defined, circular-orbit type of distribution. Nature again proves to be different on a small scale than on a macroscopic scale.
Virtual Physics
Models of the Hydrogen Atom
How did scientists figure out the structure of atoms without looking at them? Try out different models by shooting light at the atom. Use this simulation to see how the prediction of the model matches the experimental results.
Check Your Understanding
Check Your Understanding
- The positively charged alpha particles were attracted by the attractive electrostatic force from the positive nuclei of the gold atoms.
- The positively charged alpha particles were scattered by the attractive electrostatic force from the positive nuclei of the gold atoms.
- The positively charged alpha particles were scattered by the repulsive electrostatic force from the positive nuclei of the gold atoms.
- The positively charged alpha particles were attracted by the repulsive electrostatic force from the positive nuclei of the gold atoms.