Learning Objectives
Learning Objectives
By the end of this section, you will be able to do the following:
- Explain reflection from mirrors, describe image formation as a consequence of reflection from mirrors, apply ray diagrams to predict and interpret image and object locations, and describe applications of mirrors
- Perform calculations based on the law of reflection and the equations for curved mirrors
| angle of incidence | angle of reflection | central axis |
| concave mirror | convex mirror | diffused |
| focal length | focal point | geometric optics |
| law of reflection | law of refraction | ray |
| real image | specular | virtual image |
Characteristics of Mirrors
Characteristics of Mirrors
There are three ways, as shown in Figure 16.2, in which light can travel from a source to another location. It can come directly from the source through empty space, such as from the Sun to Earth. Light can travel to an object through various media, such as air and glass. Light can also arrive at an object after being reflected, such as by a mirror. In all these cases, light is modeled as traveling in a straight line, called a ray. Light may change direction when it encounters the surface of a different material (such as a mirror) or when it passes from one material to another (such as when passing from air into glass). It then continues in a straight line—that is, as a ray. The word ray comes from mathematics. Here it means a straight line that originates from some point. It is acceptable to visualize light rays as laser rays (or even science fiction depictions of ray guns).
Because light moves in straight lines, that is, as rays, and changes directions when it interacts with matter, it can be described through geometry and trigonometry. This part of optics, described by straight lines and angles, is therefore called geometric optics. There are two laws that govern how light changes direction when it interacts with matter: the law of reflection, for situations in which light bounces off matter; and the law of refraction, for situations in which light passes through matter. In this section, we consider the geometric optics of reflection.
Whenever we look into a mirror or squint at sunlight glinting from a lake, we are seeing a reflection. How does the reflected light travel from the object to your eyes? The law of reflection states: The angle of reflection, , equals the angle of incidence, . This law governs the behavior of all waves when they interact with a smooth surface, and therefore describe the behavior of light waves as well. The reflection of light is simplified when light is treated as a ray. This concept is illustrated in Figure 16.3, which also shows how the angles are measured relative to the line perpendicular to the surface at the point where the light ray strikes it. This perpendicular line is also called the normal line, or just the normal. Light reflected in this way is referred to as specular (from the Latin word for mirror: speculum).
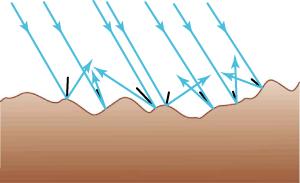
We expect to see reflections from smooth surfaces, but Figure 16.4, illustrates how a rough surface reflects light. Because the light is reflected from different parts of the surface at different angles, the rays go in many different directions, so the reflected light is diffused. Diffused light allows you to read a printed page from almost any angle because some of the rays go in different directions. Many objects, such as people, clothing, leaves, and walls, have rough surfaces and can be seen from many angles. A mirror, on the other hand, has a smooth surface and reflects light at specific angles.
When we see ourselves in a mirror, it appears that our image is actually behind the mirror. We see the light coming from a direction determined by the law of reflection. The angles are such that our image is exactly the same distance behind the mirror, di, as the distance we stand away from the mirror, do. Although these mirror images make objects appear to be where they cannot be (such as behind a solid wall), the images are not figments of our imagination. Mirror images can be photographed and videotaped by instruments and look just as they do to our eyes, which are themselves optical instruments. An image in a mirror is said to be a virtual image, as opposed to a real image. A virtual image is formed when light rays appear to diverge from a point without actually doing so.
Figure 16.5 helps illustrate how a flat mirror forms an image. Two rays are shown emerging from the same point, striking the mirror, and reflecting into the observer’s eye. The rays can diverge slightly, and both still enter the eye. If the rays are extrapolated backward, they seem to originate from a common point behind the mirror, allowing us to locate the image. The paths of the reflected rays into the eye are the same as if they had come directly from that point behind the mirror. Using the law of reflection—the angle of reflection equals the angle of incidence—we can see that the image and object are the same distance from the mirror. This is a virtual image, as defined earlier.
Fun In Physics
Mirror Mazes
Figure 16.6 is a chase scene from an old silent film called The Circus, starring Charlie Chaplin. The chase scene takes place in a mirror maze. You may have seen such a maze at an amusement park or carnival. Finding your way through the maze can be very difficult. Keep in mind that only one image in the picture is real—the others are virtual.
One of the earliest uses of mirrors for creating the illusion of space is seen in the Palace of Versailles, the former home of French royalty. Construction of the Hall of Mirrors (Figure 16.7) began in 1678. It is still one of the most popular tourist attractions at Versailles.
Only one Charlie in Figure 16.8 image is real. The others are all virtual images of him. Can you tell which is real? Hint—His hat is tilted to one side.
- The virtual images have their hats tilted to the right.
- The virtual images have their hats tilted to the left.
- The real images have their hats tilted to the right.
- The real images have their hats tilted to the left.
Watch Physics
Virtual Image
This video explains the creation of virtual images in a mirror. It shows the location and orientation of the images using ray diagrams, and relates the perception to the human eye.
- The distances of the image and the object from the mirror are the same.
- The distances of the image and the object from the mirror are always different.
- The image is formed at infinity if the object is placed near the mirror.
- The image is formed near the mirror if the object is placed at infinity.
Some mirrors are curved instead of flat. A mirror that curves inward is called a concave mirror, whereas one that curves outward is called a convex mirror. Pick up a well-polished metal spoon and you can see an example of each type of curvature. The side of the spoon that holds the food is a concave mirror; the back of the spoon is a convex mirror. Observe your image on both sides of the spoon.
Tips For Success
You can remember the difference between concave and convex by thinking, Concave means caved in.
Ray diagrams can be used to find the point where reflected rays converge or appear to converge, or the point from which rays appear to diverge. This is called the focal point, F. The distance from F to the mirror along the central axis (the line perpendicular to the center of the mirror’s surface) is called the focal length, f. Figure 16.9 shows the focal points of concave and convex mirrors.
Images formed by a concave mirror vary, depending on which side of the focal point the object is placed. For any object placed on the far side of the focal point with respect to the mirror, the rays converge in front of the mirror to form a real image, which can be projected onto a surface, such as a screen or sheet of paper However, for an object located inside the focal point with respect to the concave mirror, the image is virtual. For a convex mirror the image is always virtual—that is, it appears to be behind the mirror. The ray diagrams in Figure 16.10 show how to determine the nature of the image formed by concave and convex mirrors.
The information in Figure 16.10 is summarized in Table 16.1.
| Type of Mirror | Object to Mirror Distance, do | Image Characteristics |
|---|---|---|
| Concave | Real and inverted | |
| Concave | Virtual and erect | |
| Convex | Virtual and erect |
Snap Lab
Concave and Convex Mirrors
- Silver spoon and silver polish, or a new spoon made of any shiny metal
Instructions
- Choose any small object with a top and a bottom, such as a short nail or tack, or a coin, such as a quarter. Observe the object’s reflection on the back of the spoon.
- Observe the reflection of the object on the front (bowl side) of the spoon when held away from the spoon at a distance of several inches.
- Observe the image while slowly moving the small object toward the bowl of the spoon. Continue until the object is all the way inside the bowl of the spoon.
- You should see one point where the object disappears and then reappears. This is the focal point.
Watch Physics
Parabolic Mirrors and Real Images
This video uses ray diagrams to show the special feature of parabolic mirrors that makes them ideal for either projecting light energy in parallel rays, with the source being at the focal point of the parabola, or for collecting at the focal point light energy from a distant source.
- The rays do not polarize after reflection.
- The rays are dispersed after reflection.
- The rays are polarized after reflection.
- The rays become parallel after reflection.
You should be able to notice everyday applications of curved mirrors. One common example is the use of security mirrors in stores, as shown in Figure 16.11.
Some telescopes also use curved mirrors and no lenses (except in the eyepieces) both to magnify images and to change the path of light. Figure 16.12 shows a Schmidt-Cassegrain telescope. This design uses a spherical primary concave mirror and a convex secondary mirror. The image is projected onto the focal plane by light passing through the perforated primary mirror. The effective focal length of such a telescope is the focal length of the primary mirror multiplied by the magnification of the secondary mirror. The result is a telescope with a focal length much greater than the length of the telescope itself.
A parabolic concave mirror has the very useful property that all light from a distant source, on reflection by the mirror surface, is directed to the focal point. Likewise, a light source placed at the focal point directs all the light it emits in parallel lines away from the mirror. This case is illustrated by the ray diagram in Figure 16.13. The light source in a car headlight, for example, is located at the focal point of a parabolic mirror.
Parabolic mirrors are also used to collect sunlight and direct it to a focal point, where it is transformed into heat, which in turn can be used to generate electricity. This application is shown in Figure 16.14.
- The height of the image became infinite.
- The height of the object became zero.
- The intensity of intersecting light rays became zero.
- The intensity of intersecting light rays increased.
The Application of the Curved Mirror Equations
The Application of the Curved Mirror Equations
Curved mirrors and the images they create involve a fairly small number of variables: the mirror’s radius of curvature, R; the focal length, f; the distances of the object and image from the mirror, do and di, respectively; and the heights of the object and image, ho and hi, respectively. The signs of these values indicate whether the image is inverted, erect (upright), real, or virtual. We now look at the equations that relate these variables and apply them to everyday problems.
Figure 16.15 shows the meanings of most of the variables we will use for calculations involving curved mirrors.
The basic equation that describes both lenses and mirrors is the lens/mirror equation
This equation can be rearranged several ways. For example, it may be written to solve for focal length.
Magnification, m, is the ratio of the size of the image, hi, to the size of the object, ho. The value of m can be calculated in two ways.
This relationship can be written to solve for any of the variables involved. For example, the height of the image is given by
We saved the simplest equation for last. The radius of curvature of a curved mirror, R, is simply twice the focal length.
We can learn important information from the algebraic sign of the result of a calculation using the previous equations:
- A negative di indicates a virtual image; a positive value indicates a real image
- A negative hi indicates an inverted image; a positive value indicates an erect image
- For concave mirrors, f is positive; for convex mirrors, f is negative
Now let’s apply these equations to solve some problems.
Worked Example
Calculating Focal Length
A person standing 6.0 m from a convex security mirror forms a virtual image that appears to be 1.0 m behind the mirror. What is the focal length of the mirror?
STRATEGY
The person is the object, so do = 6.0 m. We know that, for this situation, do is positive. The image is virtual, so the value for the image distance is negative, so di = –1.0 m.
Now, use the appropriate version of the lens/mirror equation to solve for focal length by substituting the known values.
The negative result is expected for a convex mirror. This indicates the focal point is behind the mirror.
Worked Example
Calculating Object Distance
Electric room heaters use a concave mirror to reflect infrared (IR) radiation from hot coils. Note that IR radiation follows the same law of reflection as visible light. Given that the mirror has a radius of curvature of 50.0 cm and produces an image of the coils 3.00 m in front of the mirror, where are the coils with respect to the mirror?
STRATEGY
We are told that the concave mirror projects a real image of the coils at an image distance di = 3.00 m. The coils are the object, and we are asked to find their location—that is, to find the object distance do. We are also given the radius of curvature of the mirror, so that its focal length is f = R/2 = 25.0 cm (a positive value, because the mirror is concave, or converging). We can use the lens/mirror equation to solve this problem.
Because di and f are known, the lens/mirror equation can be used to find do.
Rearranging to solve for do, we have
Entering the known quantities gives us
Note that the object (the coil filament) is farther from the mirror than the mirror’s focal length. This is a case 1 image (do > f and f positive), consistent with the fact that a real image is formed. You get the most concentrated thermal energy directly in front of the mirror and 3.00 m away from it. In general, this is not desirable because it could cause burns. Usually, you want the rays to emerge parallel, and this is accomplished by having the filament at the focal point of the mirror.
Note that the filament here is not much farther from the mirror than the focal length, and that the image produced is considerably farther away.
Practice Problems
Practice Problems
What is the focal length of a makeup mirror that produces a magnification of 1.50 when a person’s face is 12.0 cm away? Construct a ray diagram using paper, a pencil and a ruler to confirm your calculation.
- –36.0 cm
- –7.20 cm
- 7.20 cm
- 36.0 cm
Check Your Understanding
Check Your Understanding
How does the object distance, do, compare with the focal length, f, for a concave mirror that produces an image that is real and inverted?
- do > f, where do and f are object distance and focal length, respectively.
- do < f, where do and f are object distance and focal length, respectively.
- do = f, where do and f are object distance and focal length, respectively.
- do = 0, where do is the object distance.
- The surface becomes smooth, and a smooth surface produces a sharp image.
- The surface becomes irregular, and an irregular surface produces a sharp image.
- The surface becomes smooth, and a smooth surface transmits light, but does not reflect it.
- The surface becomes irregular, and an irregular surface produces a blurred image.
- It is real and erect.
- It is real and inverted.
- It is virtual and inverted.
- It is virtual and erect.