Learning Objectives

By the end of this section, you will be able to do the following:

Describe the Doppler effect of sound waves
Explain a sonic boom
Calculate the frequency shift of sound from a moving object by the Doppler shift formula, and calculate the speed of an object by the Doppler shift formula

Section Key Terms
Doppler effect	sonic boom

The Doppler Effect of Sound Waves

The Doppler effect is a change in the observed pitch of a sound, due to relative motion between the source and the observer. An example of the Doppler effect due to the motion of a source occurs when you are standing still, and the sound of a siren coming from an ambulance shifts from high-pitch to low-pitch as it passes by. The closer the ambulance is to you, the more sudden the shift. The faster the ambulance moves, the greater the shift. We also hear this shift in frequency for passing race cars, airplanes, and trains. An example of the Doppler effect with a stationary source and moving observer is if you ride a train past a stationary warning bell, you will hear the bell’s frequency shift from high to low as you pass by.

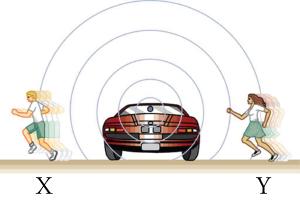
What causes the Doppler effect? Let’s compare three different scenarios: Sound waves emitted by a stationary source (Figure 14.15), sound waves emitted by a moving source (Figure 14.16), and sound waves emitted by a stationary source but heard by moving observers (Figure 14.17). In each case, the sound spreads out from the point where it was emitted.

If the source and observers are stationary, then observers on either side see the same wavelength and frequency as emitted by the source. But if the source is moving and continues to emit sound as it travels, then the air compressions (crests) become closer together in the direction in which it’s traveling and farther apart in the direction it’s traveling away from. Therefore, the wavelength is shorter in the direction the source is moving (on the right in Figure 14.16), and longer in the opposite direction (on the left in Figure 14.16).

Finally, if the observers move, as in Figure 14.17, the frequency at which they receive the compressions changes. The observer moving toward the source receives them at a higher frequency (and therefore shorter wavelength), and the person moving away from the source receives them at a lower frequency (and therefore longer wavelength).

Sounds emitted by a stationary car spread out in spherical waves as stationary observers listen on both sides.

Figure 14.15 Sounds emitted by a source spread out in spherical waves. Because the source, observers, and air are stationary, the wavelength and frequency are the same in all directions and to all observers.

Sound waves are compressed ahead of the motion of a car and stretched out in the wake of the motion of the car as stationary observers listen on both sides.

Figure 14.16 Sounds emitted by a source moving to the right spread out from the points at which they were emitted. The wavelength is reduced and, consequently, the frequency is increased in the direction of motion, so that the observer on the right hears a higher-pitch sound. The opposite is true for the observer on the left, where the wavelength is increased and the frequency is reduced.

One observer runs away from the sound source (a car) while another runs toward it.

Figure 14.17 The same effect is produced when the observers move relative to the source. Motion toward the source increases frequency as the observer on the right passes through more wave crests than she would if stationary. Motion away from the source decreases frequency as the observer on the left passes through fewer wave crests than he would if stationary.

We know that wavelength and frequency are related by $v = f λ,$ where v is the fixed speed of sound. The sound moves in a medium and has the same speed v in that medium whether the source is moving or not. Therefore, f multiplied by $λ$ is a constant. Because the observer on the right in Figure 14.16 receives a shorter wavelength, the frequency she perceives must be higher. Similarly, the observer on the left receives a longer wavelength and therefore perceives a lower frequency.

The same thing happens in Figure 14.17. A higher frequency is perceived by the observer moving toward the source, and a lower frequency is perceived by an observer moving away from the source. In general, then, relative motion of source and observer toward one another increases the perceived frequency. Relative motion apart decreases the perceived frequency. The greater the relative speed is, the greater the effect.

Watch Physics

Introduction to the Doppler Effect

This video explains the Doppler effect visually.

Click to view content

Grasp Check

If you are standing on the sidewalk facing the street and an ambulance drives by with its siren blaring, at what point will the frequency that you observe most closely match the actual frequency of the siren?

when it is coming toward you
when it is going away from you
when it is in front of you

For a stationary observer and a moving source of sound, the frequency (f_obs) of sound perceived by the observer is

14.11

f_{o b s} = f_{s} (\frac{v_{w}}{v_{w} \pm v_{s}}),

where f_s is the frequency of sound from a source, v_s is the speed of the source along a line joining the source and observer, and v_w is the speed of sound. The minus sign is used for motion toward the observer and the plus sign for motion away from the observer.

Tips For Success

Rather than just memorizing rules, which are easy to forget, it is better to think about the rules of an equation intuitively. Using a minus sign in $f_{o b s} = f_{s} (\frac{v_{w}}{v_{w} \pm v_{s}})$ will decrease the denominator and increase the observed frequency, which is consistent with the expected outcome of the Doppler effect when the source is moving toward the observer. Using a plus sign will increase the denominator and decrease the observed frequency, consistent with what you would expect for the source moving away from the observer. This may be more helpful to keep in mind rather than memorizing the fact that “the minus sign is used for motion toward the observer and the plus sign for motion away from the observer.”

Note that the greater the speed of the source, the greater the Doppler effect. Similarly, for a stationary source and moving observer, the frequency perceived by the observer f_obs is given by

14.12

f_{o b s} = f_{s} (\frac{v_{w} \pm v_{o b s}}{v_{w}}),

where v_obs is the speed of the observer along a line joining the source and observer. Here the plus sign is for motion toward the source, and the minus sign is for motion away from the source.

Sonic Booms

What happens to the sound produced by a moving source, such as a jet airplane, that approaches or even exceeds the speed of sound? Suppose a jet airplane is coming nearly straight at you, emitting a sound of frequency f_s. The greater the plane’s speed, v_s, the greater the Doppler shift and the greater the value of f_obs. Now, as v_s approaches the speed of sound, v_w, f_obs approaches infinity, because the denominator in $f_{o b s} = f_{s} (\frac{v_{w}}{v_{w} - v_{s}})$ approaches zero.

This result means that at the speed of sound, in front of the source, each wave is superimposed on the previous one because the source moves forward at the speed of sound. The observer gets them all at the same instant, and so the frequency is theoretically infinite. If the source exceeds the speed of sound, no sound is received by the observer until the source has passed, so that the sounds from the source when it was approaching are stacked up with those from it when receding, creating a sonic boom. A sonic boom is a constructive interference of sound created by an object moving faster than sound.

An aircraft creates two sonic booms, one from its nose and one from its tail (see Figure 14.18). During television coverage of space shuttle landings, two distinct booms could often be heard. These were separated by exactly the time it would take the shuttle to pass by a point. Observers on the ground often do not observe the aircraft creating the sonic boom, because it has passed by before the shock wave reaches them. If the aircraft flies close by at low altitude, pressures in the sonic boom can be destructive enough to break windows. Because of this, supersonic flights are banned over populated areas of the United States.

The first sonic boom trails behind the nose of the aircraft and the second trails behind the tail.

Figure 14.18 Two sonic booms, created by the nose and tail of an aircraft, are observed on the ground after the plane has passed by.

Solving Problems Using the Doppler Shift Formula

Watch Physics

Doppler Effect Formula for Observed Frequency

This video explains the Doppler effect formula for cases when the source is moving toward the observer.

Click to view content

Grasp Check

Let’s say that you have a rare phobia where you are afraid of the Doppler effect. If you see an ambulance coming your way, what would be the best strategy to minimize the Doppler effect and soothe your Doppleraphobia?

Stop moving and become stationary till it passes by.
Run toward the ambulance.
Run alongside the ambulance.

Watch Physics

Doppler Effect Formula When Source is Moving Away

This video explains the Doppler effect formula for cases when the source is moving away from the observer.

Click to view content

Grasp Check

Sal uses two different formulas for the Doppler effect-one for when the source is moving toward the observer and another for when the source is moving away. However, in this textbook we use only one formula. Explain.

The combined formula that can be used is, Use ( $+$ ) when the source is moving toward the observer and ( $-$ ) when the source is moving away from the observer.
The combined formula that can be used is, $f_{o b s} = f_{s} (\frac{v_{w} \pm v_{s}}{v_{w}})$ . Use ( $+$ ) when the source is moving away from the observer and ( $-$ ) when the source is moving toward the observer.
The combined formula that can be used is, $f_{o b s} = f_{s} (\frac{v_{w}}{v_{w} \pm v_{s}})$ . Use ( $+$ ) when the source is moving toward the observer and ( $-$ ) when the source is moving away from the observer.
The combined formula that can be used is, $f_{o b s} = f_{s} (\frac{v_{w}}{v_{w} \pm v_{s}})$ . Use ( $+$ ) when the source is moving away from the observer and ( $-$ ) when the source is moving toward the observer.

Worked Example

Calculate Doppler Shift: A Train Horn

Suppose a train that has a 150 Hz horn is moving at 35 m/s in still air on a day when the speed of sound is 340 m/s. What frequencies are observed by a stationary person at the side of the tracks as the train approaches and after it passes?

Strategy

To find the observed frequency, $f_{o b s} = f_{s} (\frac{v_{w}}{v_{w} \pm v_{s}})$ must be used because the source is moving. The minus sign is used for the approaching train, and the plus sign for the receding train.

Solution

(1) Enter known values into $f_{o b s} = f_{s} (\frac{v_{w}}{v_{w} - v_{s}})$ to calculate the frequency observed by a stationary person as the train approaches:

$f_{o b s} = f_{s} (\frac{v_{w}}{v_{w} - v_{s}}) = (150 Hz) (\frac{340 m/s}{340 m/s - 35 m/s})$ $= 167 Hz \approx 170 Hz (2 sig. figs.)$

(2) Use the same equation but with the plus sign to find the frequency heard by a stationary person as the train recedes.

$f_{o b s} = f_{s} (\frac{v_{w}}{v_{w} + v_{s}}) = (150 Hz) (\frac{340 m/s}{340 m/s + 35 m/s})$ $= 136 Hz \approx 140 Hz (2 sig. figs.)$

Discussion

The numbers calculated are valid when the train is far enough away that the motion is nearly along the line joining the train and the observer. In both cases, the shift is significant and easily noticed. Note that the shift is approximately 20 Hz for motion toward and approximately 10 Hz for motion away. The shifts are not symmetric.

Practice Problems

What is the observed frequency when the source having frequency

3.0 kHz

is moving towards the observer at a speed of

1.0 \times 10^{2} m / s

and the speed of sound is

331 m/s

?

$3.0 kHz$
$3.5 kHz$
$2.3 kHz$
$4.3 kHz$

A train is moving away from you at a speed of

50.0 m/s

. If you are standing still and hear the whistle at a frequency of

305 Hz

, what is the actual frequency of the produced whistle? (Assume speed of sound to be

331 m/s

.)

$259 Hz$
$205 Hz$
$405 Hz$
$351 Hz$

Check Your Understanding

Exercise 11

What is the Doppler effect?

The Doppler effect is a change in the observed speed of a sound due to the relative motion between the source and the observer.
The Doppler effect is a change in the observed frequency of a sound due to the relative motion between the source and the observer.
The Doppler effect is a change in the observed intensity of a sound due to the relative motion between the source and the observer.
The Doppler effect is a change in the observed timbre of a sound, due to the relative motion between the source and the observer.

Exercise 12

Give an example of the Doppler effect caused by motion of the source.

The sound of a vehicle horn shifts from low-pitch to high-pitch as we move towards it.
The sound of a vehicle horn shifts from low-pitch to high-pitch as we move away from it.
The sound of a vehicle horn shifts from low-pitch to high-pitch as it passes by.
The sound of a vehicle horn shifts from high-pitch to low-pitch as it passes by.

Exercise 13

What is a sonic boom?

It is a destructive interference of sound created by an object moving faster than sound.
It is a constructive interference of sound created by an object moving faster than sound.
It is a destructive interference of sound created by an object moving slower than sound.
It is a constructive interference of sound created by an object moving slower than sound.

Exercise 14

What is the relation between speed of source and value of observed frequency when the source is moving towards the observer?

They are independent of each other.
The greater the speed, the greater the value of observed frequency.
The greater the speed, the smaller the value of observed frequency.
The speed of the sound is directly proportional to the square of the frequency observed.

14.3 Doppler Effect and Sonic Booms

Learning Objectives